Bonjour, je suis en bachelor informatique et cybersécurité donc j'ai besoin des mathématiques ...
j'aimerai savoir comment résoudre un système de congruence :
n ≡ 2 [7]
n ≡ 5 [9]
Notre professeur nous dit que l'on doit trouver la solution particulière et enfin la solution générale.
Merci de votre réponse
Congruence
7 messages
- Page 1 sur 1
Re: congruence
Bonjour,
Le théorème des restes chinois, ça ne te dit rien ?
Tu peux remarquer que 7 et 9 sont premiers entre eux. Une identité de Bézout entre 7 et 9 ?
Ou alors, au ras des pâquerettes : veut dire
veut dire 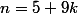 avec
avec 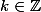 . Essaie des
. Essaie des  jusqu'à en trouver un qui donne un
jusqu'à en trouver un qui donne un  congru à 2 modulo 7. Tu auras alors une solution particulière.
congru à 2 modulo 7. Tu auras alors une solution particulière.
Le théorème des restes chinois, ça ne te dit rien ?
Tu peux remarquer que 7 et 9 sont premiers entre eux. Une identité de Bézout entre 7 et 9 ?
Ou alors, au ras des pâquerettes :
Re: congruence
La solution au ras des pâquerettes me semble la plus adaptée quand on n'est pas à l'aise en maths. Et même quand on est plus ou moins à l'aise.
Mais déjà, la première étape, c'est de savoir donner quelques exemples de nombres qui vérifient n ≡ 2 [7]
, et quelques autres exemples, pour n ≡ 5 [9]
Une dizaine de nombres dans chacune de ces 2 séries.
Si on sait faire ça, sereinement, alors la suite vient naturellement.
Mais déjà, la première étape, c'est de savoir donner quelques exemples de nombres qui vérifient n ≡ 2 [7]
, et quelques autres exemples, pour n ≡ 5 [9]
Une dizaine de nombres dans chacune de ces 2 séries.
Si on sait faire ça, sereinement, alors la suite vient naturellement.
Re: congruence
Je suis un spécialiste du ras des pâquerettes :
Un congruence modulo 9 se calcule en itérant la somme des chiffres .
Donc on part des congruences à 2 modulo 7 : 2,9,16,23 bingo! 2+3=5
Donc n=23 est solution particulière .
Un congruence modulo 9 se calcule en itérant la somme des chiffres .
Donc on part des congruences à 2 modulo 7 : 2,9,16,23 bingo! 2+3=5
Donc n=23 est solution particulière .
Re: congruence
GaBuZoMeu a écrit:Bonjour,
Le théorème des restes chinois, ça ne te dit rien ?
Tu peux remarquer que 7 et 9 sont premiers entre eux. Une identité de Bézout entre 7 et 9 ?
Ou alors, au ras des pâquerettes :veut dire
avec
. Essaie des
jusqu'à en trouver un qui donne un
congru à 2 modulo 7. Tu auras alors une solution particulière.
Enfaite, j'ai assez bien compris comment faire, en solution particulière je trouve :
2*9 - 7*3 = -3 ce qui fait x = 9 et y = 3 (je met x et y sinon je me perd)
et pour la solution générale, j'ai trouvé x(qui remplace l) = -3 + 2/3*k et y(remplace k) = -7/3*k+9
mais je trouve ma solution générale un peu bizarre et je ne sais s'il y a un moyen de vérifier ça...
Re: congruence
Pour la soluce particulière , je t'ai montré mieux que ça .
Avec cette soluce 23 , tu as :
n congru 2 mod 7 ssi ( n-23) congru 0 mod 7
n congru 5 mod 9 ssi (n-23) congru 0 mod 9
autrement dit , ton système est équivalent à : n - 23 est multiple de 7 et de 9 .
A toi de jouer ...
Avec cette soluce 23 , tu as :
n congru 2 mod 7 ssi ( n-23) congru 0 mod 7
n congru 5 mod 9 ssi (n-23) congru 0 mod 9
autrement dit , ton système est équivalent à : n - 23 est multiple de 7 et de 9 .
A toi de jouer ...
Re: congruence
tournesol a écrit:Pour la soluce particulière , je t'ai montré mieux que ça .
Avec cette soluce 23 , tu as :
n congru 2 mod 7 ssi ( n-23) congru 0 mod 7
n congru 5 mod 9 ssi (n-23) congru 0 mod 9
autrement dit , ton système est équivalent à : n - 23 est multiple de 7 et de 9 .
A toi de jouer ...
Oui je sais, mais c'est ce qu'on me demande de faire, avec 23 j'ai compris mais j'ai pas le choix de trouver la solution particulière et ensuite trouver la solution générale
sinon merci beaucoup pour le tuyau
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
