Congruence et classe d'équivalence

[eltheola]

Bonjour,
J'ai eu cet exercice en Td et je ne comprends vraiment pas comment le résoudre. Dans le corrigé du 1) on trouve que la classe de 1998 est égale à celle de -1 ce que je ne comprends vraiment pas. On nous dit ensuite que la classe de -999 est égale à celle de 1000, je n'y comprends rien.


1) 999 · 1998 dans Z1999 2) 136^7 dans Z137 3) 2792^217 dans Z5 4) 10^1000 dans Z13

[GaBuZoMeu]

Bonjour,
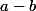
Les entiers et ont même classe modulo (on dit aussi "sont congrus modulo ") si et seulement si divise leur différence . C'est la définition.

Donc 1998 est congru à -1 modulo 1999 car 1998-(-1)= 1999.
Ils sont aussi congrus à -2000 car 1998-(-2000) = 2x1999

De même -999 est congru à 1000 (toujours modulo 1999) car -999-1000 = -1999.

[eltheola]

Merci beaucoup tout est bien plus clair maintenant !

[eltheola]

Pourriez-vous aussi m'aider à comprendre cet exercice ?

[eltheola]

Pourriez-vous aussi m'aider à comprendre cet exercice ?

:Montrer que 13 divise 2^70 + 3^70

[GaBuZoMeu]

Bonsoir,

Il faut que tu commences par potasser sérieusement ton cours, dans lequel tu as sans doute le petit théorème de Fermat : si est un nombre premier, alors pour tout entier non divisible par , est congru à 1 modulo .