Combinatoire !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ribéry_
- Membre Naturel
- Messages: 10
- Enregistré le: 13 Juil 2006, 10:02
-
 par ribéry_ » 27 Juil 2006, 09:37
par ribéry_ » 27 Juil 2006, 09:37
Bonjour , en relisant mon cahier de maths je suis tombé sur un exo dont je ne comprends pas bien la résolution ni le résultat !
Alors on dispose de n boules et de p tiroirs , combien a t-on de configurations possibles sachant qu'on peut avoir des tiroirs vides ?
Merci !
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 27 Juil 2006, 11:11
par haydenstrauss » 27 Juil 2006, 11:11
Tu peux nous montrer la resolution ? peut eter que qq comprendra :we:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 27 Juil 2006, 11:45
par aviateurpilot » 27 Juil 2006, 11:45
1er methode:soit
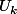
le nombre de façon pour disposer k boules dans p tiroirs sachant peut avoir des tiroirs vides.

(car pour la boule qu'on doit ajouter, on a p choix)
et on a
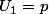
donc

-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 27 Juil 2006, 11:48
par aviateurpilot » 27 Juil 2006, 11:48
2eme methode:pour la premier boule on a p choix
pour la 2eme boule on a pchoix
.....
.....
pour la n-eme boule on a p choix
donc

-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 27 Juil 2006, 11:53
par aviateurpilot » 27 Juil 2006, 11:53
3eme methode:c'est le nombre d'applications de l'ensemble des boules vers l'ensemble des tiroirs
card(l'ensemble des tiroirs)^card(l'ensemble des boules)=

-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 27 Juil 2006, 13:01
par El_Gato » 27 Juil 2006, 13:01
Les boules sont discernables ou pas ?
Parceque si elles sont indiscernables, la réponse n'est pas
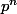
.
-
El_Gato
- Membre Relatif
- Messages: 313
- Enregistré le: 09 Fév 2006, 17:07
-
 par El_Gato » 27 Juil 2006, 13:04
par El_Gato » 27 Juil 2006, 13:04
Les boules sont discernables ou pas ?
Parceque si elles sont indiscernables, la réponse n'est pas
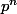
.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 27 Juil 2006, 13:40
par aviateurpilot » 27 Juil 2006, 13:40
dons ce cas,
c'est le nombre de facon pour qu'on ecrit n sous form d'une somme de p nombres (sachant qu'on peut utilisé les 0 et on peut repeter un nombre)
-
ribéry_
- Membre Naturel
- Messages: 10
- Enregistré le: 13 Juil 2006, 10:02
-
 par ribéry_ » 27 Juil 2006, 17:10
par ribéry_ » 27 Juil 2006, 17:10
euh dans ma version le prof a donné ( n+p-1 p-1 ) (c'est une binomiale , p-1 parmi n+p-1)
en disant qu'il fallait en fait voir comment placer p-1 séparations parmi les boules !
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 27 Juil 2006, 18:51
par aviateurpilot » 27 Juil 2006, 18:51
Les boules sont discernables
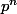
Les boules sont in discernables

-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 27 Juil 2006, 19:11
par Alpha » 27 Juil 2006, 19:11
Salut, vous pouvez aussi aller voir mon message qui se trouve sur
CETTE PAGEBien cordialement
-
ribéry_
- Membre Naturel
- Messages: 10
- Enregistré le: 13 Juil 2006, 10:02
-
 par ribéry_ » 27 Juil 2006, 20:08
par ribéry_ » 27 Juil 2006, 20:08
Le truc que je pige pas c'est le n+k-1 car ok c'est le nombre de boules + le nombre de séparations mais pourquoi piocher k-1 trucs la dedans ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 111 invités
