Comatrice
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
par chelsea-asm » 24 Oct 2012, 20:45
Bonjour,
J'ai un petit souci concernant la définition de la comatrice. Je ne la comprends pas tout à fait.
La propriété dit que
 = (-1)^{i+j} \det(A_{ij}))
où
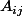
est la matrice carrée d'ordre n-1 obtenue à partir de A, en ôtant sa i-ème ligne et sa j-ème colonne.
Je me suis fait mon propre exemple.
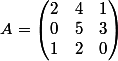
Donc
 = (-1)^4 \det(A_{22}) = \begin{vmatrix}2&1\\1&0\end{vmatrix} = -1)
Mais j'ai aussi
 = (-1)^2 \det(A_{11}) = \begin{vmatrix}5&3\\2&0\end{vmatrix} = -6)
Pourtant ma matrice est bien inversible, puisque
 \neq 0)
Dans ce cas, que vaut com(A), il n'a pas de valeur exacte ?
Je dois me tromper quelque part ou oublier une hypothèse non ?
Merci de vos réponses !
Alex
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
par cuati » 24 Oct 2012, 20:49
chelsea-asm a écrit:Bonjour,
J'ai un petit souci concernant la définition de la comatrice. Je ne la comprends pas tout à fait.
La propriété dit que
où
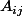
est la matrice carrée d'ordre n-1 obtenue à partir de A, en ôtant sa i-ème ligne et sa j-ème colonne.
Je me suis fait mon propre exemple.
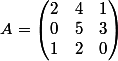
Donc
Mais j'ai aussi
Pourtant ma matrice est bien inversible, puisque
Dans ce cas, que vaut com(A), il n'a pas de valeur exacte ?
Je dois me tromper quelque part ou oublier une hypothèse non ?
Merci de vos réponses !
Alex
Bonsoir,
com(A) n'est pas un nombre, mais une matrice...
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
par chelsea-asm » 24 Oct 2012, 20:50
chelsea-asm a écrit:Je dois me tromper quelque part
Je viens en fait de comprendre que com(A) est une matrice, et que chaque coefficient en i,j est défini par la formule donnée précédemment.
Désolé pour le message "inutile" :S je cherchais depuis un petit bout de temps avant de trouver là !
Merci quand même, bonne soirée
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
par chelsea-asm » 24 Oct 2012, 20:51
cuati a écrit:Bonsoir,
com(A) n'est pas un nombre, mais une matrice...
Oui en effet, merci beaucoup, ça explique tout ^^ !
Bonne soirée
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
par cuati » 24 Oct 2012, 20:57
chelsea-asm a écrit:Oui en effet, merci beaucoup, ça explique tout ^^ !
Bonne soirée
Bonne soirée à toi aussi :lol3:
-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
par capitaine nuggets » 24 Oct 2012, 20:59
Salut !
Attention
)
est une matrice.
Si on a par exemple
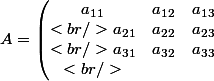
alors
= \begin{pmatrix} \alpha_{11} & \alpha_{12}& \alpha_{13} \\<br />\alpha_{21} & \alpha_{22}& \alpha_{23} \\<br />\alpha_{31} & \alpha_{32}& \alpha_{33} \\<br />\end{matrix})
où
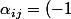^{i+j} M_{ij})
où
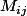
est un mineur de
privé de la ligne
et de la colonne
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
