Chapitre:# integrale de Lebesgue
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fourize
- Membre Rationnel
- Messages: 563
- Enregistré le: 26 Oct 2008, 00:40
-
par fourize » 02 Jan 2010, 21:36
bonsoir !
je suis entrain de réviser ce chapitre et je rencontre quelques petites subtilités que je vais vous poser comme questions histoire de m'éclairer :zen:
Q:1. que signifie une fonction g est égale à une fonction f presque partout ?
* prenons un exemple:
soit
 = e^x,)
si
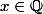
et
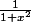
sinon
on me demande de déterminer une fonction g IR---> IR, continue telle que
f = g presque partout . comment faire?
merci d'avance de votre aide !
P.S. j'ai une correction de cet exo qui dit que g =
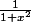
si ça peut aider ! :zen:
* In God we trust, for all others bring data *
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 02 Jan 2010, 21:54
Bonsoir : :happy3:
est agale à
presque partout signifie que $
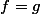
en dehors d'un ensemble negligeable
( i.e : $
 = 0 $)
)!
Autrement dit :
: $
 \neq g(x) $)
Par contre :
: $
 = g(x) $)
Cordialement ! :happy3:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
par barbu23 » 02 Jan 2010, 22:04
Pour la suite de ta question : :happy3:
Tu as :
 = \frac{1}{x^2 +1} $)
.
En effet :
est continue.
De l'autre coté :
$ \forall x \in \mathbb{R} \backslash \mathbb{Q} $ : $ g(x) = f(x) = \frac{1}{x^{2}+1} $
:
 = \frac{1}{x^2 +1} \neq f(x) = e^{x} $)
et
 = \lambda(\bigcup_{x \in \mathbb{Q}} \{ x \} )= \sum_{x \in \mathbb{Q}} \lambda(\{ x \}) = \sum_{x \in \mathbb{Q}} 0 = 0 + ... + = 0 $)
:happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
