Changement de variables, intégrales doubles [résolu merci a moi même]

[Daft Punk]

Bonjour, voici un exercice qui me pose probleme, j'espere que vous pourrez m'aider.

Soit intégrale double sur D de (x²+y²)dx dy,

où D={(x,y)appartenant a R²; 0
1) Représenter graphiquement le domaine D.

2) A l'aide du changement de variables u=xy et v=y/x, calculer la valeur de cette intégrale.

désolé mais je n'ai pas trouvé les fonctions permettant d'utiliser les symboles mathématiques.

Merci d'avance.

[jeje56]

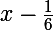
D est délimité par les droites d'équations y=1, x=1, et

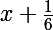
En effet, pour les deux dernières :

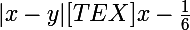
<=y<=

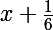
[Daft Punk]

désolé, petite erreur dans l'énoncé, c'était trop simple comme ca :cry:
j'édite mon post.
merci pour ta réponse quand meme :we:

[jeje56]

Lol, j'avoue que ça n'a plus rien à voir...

[Joker62]

Bé

1 <= y/x <= 3 <=> x <= y <= 3x
1 <= xy <= 4 <=> 1/x <= y <= 4/x

Suffit de tracer les fonctions appropriées et d'hachurer D...

[Daft Punk]

il suffit il suffit... facile a dire...
il suffit de résoudre l'exercice aussi.
un schéma peut aider, mais ca n'est pas la résolution du probleme.
On doit utiliser le jacobien etc pour le changement de variable, bien redéfinir les bornes

[Joker62]

Je ne résolvais pas le problème, j'aidais à la question 1)...
Les équivalences me semblent claires... Enfin assez claire pour s'attaquer à une histoire d'intégrale double.
La deuxième question, c'est autre chose c'est sûr, autant commencer dans l'ordre non ?

[Daft Punk]

oui il faut faire dans l'ordre, mais faire un graphique de ce niveau est encore a ma portée
merci pour l'aide quand meme

passons a la question 2 maintenant, qui est beaucoup plus problematique :mur:

[Joker62]

Bon ben attaquant la question 2 ensemble alors :)

On cherche à calculer l'intégrale de f(x,y) = x^2 + y^2 sur le domaine D
L'exercice propose le changement de variable Phi(x,y) = (u,v) = (xy;y/x)

La question 1) nous donne clairement que Phi(D) = [1;4]x[1;3] qui est donc un domaine rectangle beaucoup plus simple à manier.

Donc les étapes :
Calculer le jacobien de Phi
Utiliser le théorème général du changement de variable.
Si t'arrive pas j'suis là.

Je trouve 420 moi :^)

[Daft Punk]

sur un domaine [1:4]*[1;3] tu trouves 420 ?!?!
il faudrait avoir une fonction "grande".

j'ai finalement réussi, j'ai trouvé 10, le resultat me semble cohérent

merci a tous pour votre aide :we:

[Joker62]

Lol :D me suis ptète trompé vui c'est possible :D mais la fonction va quand même loin sur ce domaine :) enfin je sais pas montre ta résolution pour voir

[Daft Punk]

on commence par exprimer x et y en fonction de u et v, on trouve x=racine de (u/v) et y= racine de (u*v)

ensuite en faisant le jacobien du changement de variable, je trouve J=1/2v

ensuite je repasse a l'intégrale double:

on a donc intégrale double sur D de (u/v + u*v)/(2v) du dv

D devient ainsi rectangle [1:4]*[1;3] comme tu l'avais dis, on se ramene au calcul de 2 intégrales simples successives, calcul bete et méchant, on arrive finalement a 10 si je ne me suis pas trompé.