Changement de repère 3D vers 2D.

[sonizef]

Bonjour, dans le cadre de mon stage j'aurai une question à vous posez.
En gros je bloqué à un changement de repère (pour passer d'un repère 3D vers un repère 2D). :help:

Je poste dans le section supérieur mais peut être que je m'emballe, c'est juste que je suis en BTS et que je ne sais pas faire ça (pour ma défense j'ai pas souvenir d'avoir abordé ce sujet en maths ^^')

Donc si vous pouviez faire le plus simple possible :)

Afin de vous situez un peu dans le contexte c'est que j'ai une pièce en 3D formés de plusieurs triangles, et quand je clique sur l'un des triangles je voudrais le mettre à "plat" (sur Z = 0) mais il faut que X et Y subissent une transformation pour pas les déformer.

Ici l'exemple est simplifié à 3 points avec des coordonnés sous forme d'entier, dans le cas réel c'est composé de 5 ou 20 points avec des coordonnées en float. (Je précise au cas ou ça changerai quelques choses aux calculs). :triste:

Exemple :

Nous avons ces 9 valeurs (3 coordonnés de 3 points.)

Pts / X / Y / Z /
1 / 10 / 5 / 3 /
2 / 8 / 2 / 2 /
3 / 3 / 7 / 1 /

Cela forme donc un plan en positionné sur dans l'espace. ( Je me trompe pas au moins :we: ?)

:!: Seulement voilà j'ai besoin de "supprimer" l'axe Z et ainsi ramener ce plan à plat en 2D. :mur:

Depuis 2 jours je cherche sur Internet (je suis même tombé sur votre site mais les explications me semblaient bien compliquées ou ce n'était pas ce que je cherchais exactement) :mur: :mur:

De ce que j'ai compris on doit trouver (ou calculer 2 vecteurs) puis les appliquer aux valeurs ? :hein:

J'espère avoir étais assez compréhensible.

En vous remerciant ...

[Mathusalem]

Tu as une grande liberté pour ce faire, puisque tu vas pouvoir placer tes axes où tu le souhaites et orientés comme tu le souhaites, dans le plan.

Le plus simple est par exemple de poser le point 1 en (0,0).
Calcule ensuite la distance entre le point 1 et le point 2. Elle vaut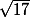 sauf erreur.

Tu peux alors placer le point 2 en ou .

Pour le 3ème point, je vais te laisser réfléchir .

Un dessin, c'est toujours bien pour donner des idées.

[sonizef]

Tu as une grande liberté pour ce faire, puisque tu vas pouvoir placer tes axes où tu le souhaites et orientés comme tu le souhaites, dans le plan.

Le plus simple est par exemple de poser le point 1 en (0,0).
Calcule ensuite la distance entre le point 1 et le point 2. Elle vaut sauf erreur.

Tu peux alors placer le point 2 en ou .

Pour le 3ème point, je vais te laisser réfléchir .

Un dessin, c'est toujours bien pour donner des idées.

Merci pour la réponse.
Seulement le , comment est ce que tu le trouve ? Après je pense que le pouvoir trouver le 3ème point devrait être assez simple.

[raph107]

Merci pour la réponse.
Seulement le , comment est ce que tu le trouve ? Après je pense que le pouvoir trouver le 3ème point devrait être assez simple.

est la norme du vecteur AB mais il me semble que Mathusalem a fait une erreur de calcul, je trouve

[Black Jack]

Il y a une infinité de façon de ramener une figure dans un plan donné.
En effet, si on a une solution, on peut toujours la translater ou la faire pivoter dans le plan et on a une autre position pour les points.

Par contre, les distances sont inchangées entre les sommets.

A(10;5;3)
B(8;2;2)
C(3;7;1)

AB = V(2²+3²+1²) = V14
AC = V(7²+2²+2²) = V57
BC = V(5²+5²+1²) = V51

Une solution est alors, par exemple, de placer A'(0 ; 0 ; 0), B' = (0 ; V14 ; 0) et C'(X ; Y ; 0) et calculer les valeurs de X et Y pour que les longueurs soient respectées.

A'C' = V(X² + Y²) = V57
B'C' = V(X² + (Y - V14)²) = V51

X² + Y² = 57
X² + (Y - V14)² = 51

X² + Y² = 57
X² + Y² + 14 - 2V14 * Y = 51

57 + 14 - 2V14 * Y = 51
2V14 * Y = 20
Y = 10/V14

X² = 57 - Y²
X² = 57 - 100/14 = 698/14 = 349/7
X = +/- V(349/7)

On a donc 2 possibilités pour C' ; C'(-V(349/7) ; 10/V14 ; 0) et C'(V(349/7) ; 10/V14 ; 0)

Avec A'(0 ; 0 ; 0), B' = (0 ; V14 ; 0)

A'B'C' est une représentation dans le plan OXY du triangle ABC... ou une représentation de son "miroir".
Il reste quelque chose à faire pour choisir le signe de X, si on veut distinguer le sens (direct ou indirect) de A'B'C'... si cela a un sens.

Et bien entendu, toute translation ou rotation de A'B'C' dans le plan OXY est tout aussi valable.


Toutes erreurs incluses.

:zen:

[ampholyte]

Bonjour,

Soit et deux points d'un repère R. La distance AB se calcule par :



PS : Je trouve également entre le point 1 et 2

[sonizef]

Merci à tous pour vos réponses !

Je pense avoir trouvé ce qu'il me fallait, et rapidement ! :D

Je vais donc essayer tout ça mais ça m'a l'air compréhensible

[sonizef]

Il y a une infinité de façon de ramener une figure dans un plan donné.
En effet, si on a une solution, on peut toujours la translater ou la faire pivoter dans le plan et on a une autre position pour les points.

Par contre, les distances sont inchangées entre les sommets.

A(10;5;3)
B(8;2;2)
C(3;7;1)

AB = V(2²+3²+1²) = V14
AC = V(7²+2²+2²) = V57
BC = V(5²+5²+1²) = V51

Une solution est alors, par exemple, de placer A'(0 ; 0 ; 0), B' = (0 ; V14 ; 0) et C'(X ; Y ; 0) et calculer les valeurs de X et Y pour que les longueurs soient respectées.

A'C' = V(X² + Y²) = V57
B'C' = V(X² + (Y - V14)²) = V51

X² + Y² = 57
X² + (Y - V14)² = 51

[•••]

:zen:

J'aurai une question à ce niveau ...
Si j'ai un point D et E en plus par exemple, comment faire ?

A'D' et B'D' ou bien B'D' et C'D' ?

Voilà je pose toute ces questions parce que je voudrais pour le moment le mettre dans un tableau qui va automatiser ce calcul ... Je vais vous poster l'exemple du tableau
Merci

[Black Jack]

J'aurai une question à ce niveau ...
Si j'ai un point D et E en plus par exemple, comment faire ?

A'D' et B'D' ou bien B'D' et C'D' ?

C'est normal ou je me suis trompé ?

Merci

Si plus de 3 points, il faut commencer par vérifier si tous les points sont bien coplanaires.

Soit par exemple 4 points A,B,C et D connus par leurs coordonnées.

a) Vérifier si les points son coplanaires. Si ce n'est pas le cas, c'est fini, il n'y a pas de solution.

b) Si les points sont bien coplanaires, on peut calculer les distances : AB , AC , AD , BC , BD , CD

On peut ensuite à partir des mesures AB et AC, placer les points A' et B' comme dans l'exemple à 3 points (en se servant des distances AC et BC)

- Ceci fait on calcule les positions possible pour C' ... comme dans le cas à 3 points.

- On calcule ensuite (avec A' et B' fixés) les positions possibles pour D' (de la même manière qu'avec C'), on utilise pour cela les distances AD et BD

Reste à choisir entre les 2 positions possible pour C' et les 2 positions possibles pour D'
On devrait pouvoir trancher en calculant les distances C'D' qui doit valoir la distance CD.

On peut ainsi pouvoir appliquer le procédé pour plus de points, mais cela devient vite pénible.
***********

Remarque que cette complication n'existe pas dans la résolution du problème initial, qui était :

"j'ai une pièce en 3D formés de plusieurs triangles, et quand je clique sur l'un des triangles je voudrais le mettre à "plat" (sur Z = 0)"

Chaque "triangle" est bien entendu une figure plane déterminée par ses 3 sommets et il n'y a alors pas de difficulté à mettre "à plat" n'importe lequel de ces triangles.

:zen:

[sonizef]

Si plus de 3 points, il faut commencer par vérifier si tous les points sont bien coplanaires.

Soit par exemple 4 points A,B,C et D connus par leurs coordonnées.

a) Vérifier si les points son coplanaires. Si ce n'est pas le cas, c'est fini, il n'y a pas de solution.

b) Si les points sont bien coplanaires, on peut calculer les distances : AB , AC , AD , BC , BD , CD

On peut ensuite à partir des mesures AB et AC, placer les points A' et B' comme dans l'exemple à 3 points (en se servant des distances AC et BC)

- Ceci fait on calcule les positions possible pour C' ... comme dans le cas à 3 points.

- On calcule ensuite (avec A' et B' fixés) les positions possibles pour D' (de la même manière qu'avec C'), on utilise pour cela les distances AD et BD

Reste à choisir entre les 2 positions possible pour C' et les 2 positions possibles pour D'
On devrait pouvoir trancher en calculant les distances C'D' qui doit valoir la distance CD.

On peut ainsi pouvoir appliquer le procédé pour plus de points, mais cela devient vite pénible.
***********

Remarque que cette complication n'existe pas dans la résolution du problème initial, qui était :

"j'ai une pièce en 3D formés de plusieurs triangles, et quand je clique sur l'un des triangles je voudrais le mettre à "plat" (sur Z = 0)"

Chaque "triangle" est bien entendu une figure plane déterminée par ses 3 sommets et il n'y a alors pas de difficulté à mettre "à plat" n'importe lequel de ces triangles.

:zen:

J'avais parlé de triangle à la base pour simplifier, mais en réalité ce sont des formes quelconques ...

Tableau ICI

La A Colonne indique le nom des points qui forment ma forme (a,b,c,etc ...)
La colonne B, C et D sont les coordonnés de mes points en 3D.
La colonne F, G, et H sont mes nouvelles coordonnés de points pour la mise à "plat".

Je suppose que tous les points sont coplanaire puisque sur mon logiciel 3D cela me donne bien une forme (après je peux être à coté de la plaque ^^' )

Donc si tu peux regarder mon Excel peut-être que tu comprendra mieux, ou si tu peux modifier mes formules si elles sont fausses ?

Parce que j'ai un peu de mal à comprendre, et je pense que ça sera plus simple pour toi en ayant le tableau sous les yeux ^^

On peut ainsi pouvoir appliquer le procédé pour plus de points, mais cela devient vite pénible.

Tu me rassure pas, puisque à certain moment je dépasse les 25 points.

PS : ne fait pas attention aux couleurs sur le dessin c'est pour m'aider à voir quelles faces ont quelles points en commun ^^

[sonizef]

Tu a écris plus haut qu'il y'a un infinité de possibilité pour redresser une face, pense-tu qu'une autre faciliterai l'automatisation des formules, ou au moins simplifierai pour les cas avec plus de 25 points (enfin peut importe le nombre de point une fois automatisé ^^)

[Mathusalem]

Si tu es certain que tes points sont tous coplanaires, alors c'est assez simple de faire un algorithme qui te met la figure à plat. Parcontre, faut savoir un peu manipuler les vecteurs.


Tu prends 2 points :
1. Un point constitue l'origine du ton nouveau repère.
2. Tu prends un hasard un deuxième point, et le vecteur Point1-Point2 constitue ton axe x. Pour des raisons pratiques, il est utile que tu renormalizes ce vecteur pour que sa norme vaille 1. C'est-à-dire que tu divises toutes les composantes du vecteur par sa norme.
3. Tu construis un vecteur orthogonal à ton vecteur 'axe x' (par produit scalaire p.ex), que tu vas normaliser, et appeler l'axe y.

4. L'ordinateur ensuite relie : ton point d'origine à tous les autres points pour créér les vecteurs relatifs à l'origine que tu as choisie. Puis il calcule les projections sur le vecteur 'axe x' et le vecteur 'axe y'. En gros, tu vas calculer comment chaque vecter peut s'écrire comme somme du vecteur 'axe x' et du vecteur 'axe y'. Les coefficients devant 'axe x' et 'axe y' seront tes coordonnées dans le plan.

[sonizef]

Si tu es certain que tes points sont tous coplanaires, alors c'est assez simple de faire un algorithme qui te met la figure à plat. Parcontre, faut savoir un peu manipuler les vecteurs.


Tu prends 2 points :
1. Un point constitue l'origine du ton nouveau repère.
2. Tu prends un hasard un deuxième point, et le vecteur Point1-Point2 constitue ton axe x. Pour des raisons pratiques, il est utile que tu renormalizes ce vecteur pour que sa norme vaille 1. C'est-à-dire que tu divises toutes les composantes du vecteur par sa norme.
3. Tu construis un vecteur orthogonal à ton vecteur 'axe x' (par produit scalaire p.ex), que tu vas normaliser, et appeler l'axe y.

4. L'ordinateur ensuite relie : ton point d'origine à tous les autres points pour créér les vecteurs relatifs à l'origine que tu as choisie. Puis il calcule les projections sur le vecteur 'axe x' et le vecteur 'axe y'. En gros, tu vas calculer comment chaque vecter peut s'écrire comme somme du vecteur 'axe x' et du vecteur 'axe y'. Les coefficients devant 'axe x' et 'axe y' seront tes coordonnées dans le plan.

Merci de ta réponse, ton idée semble intéressante et plus "automatisable" ..
Seulement voilà j'ai 2 questions :

1) Comment être sur que mes points sont coplanaires ?
2) Est ce que tu pourrai me faire un exemple parce que j'ai un peu de mal à tout saisir :hein:

Si tu a besoin des points de manière concrète pour voir si cela fonctionne, j'ai mis mon tableur avec un avec 3 formes composé de plusieurs points chacune.

Merci pour votre aide.

[Black Jack]

J'avais parlé de triangle à la base pour simplifier, mais en réalité ce sont des formes quelconques ...

Tableau ICI

La A Colonne indique le nom des points qui forment ma forme (a,b,c,etc ...)
La colonne B, C et D sont les coordonnés de mes points en 3D.
La colonne F, G, et H sont mes nouvelles coordonnés de points pour la mise à "plat".

Je suppose que tous les points sont coplanaire puisque sur mon logiciel 3D cela me donne bien une forme (après je peux être à coté de la plaque ^^' )

Donc si tu peux regarder mon Excel peut-être que tu comprendra mieux, ou si tu peux modifier mes formules si elles sont fausses ?

Parce que j'ai un peu de mal à comprendre, et je pense que ça sera plus simple pour toi en ayant le tableau sous les yeux ^^



Tu me rassure pas, puisque à certain moment je dépasse les 25 points.

PS : ne fait pas attention aux couleurs sur le dessin c'est pour m'aider à voir quelles faces ont quelles points en commun ^^

J'ai effectivement trouvé ceci :

A' 0,000000000000000 0,000000000000000 0,000000000000000
B' 0,000000000000000 0,597152735161263 0,000000000000000
C' 0,297978669282412 0,535932666517066 0,000000000000000

Mais avec la réserve que Xc' pourrait aussi bien être -0,297978669282412
On prend le signe qu'on veut a priori.

On recommence comme si on avait que les points ABD
Et on trouve par la même méthode les coordonnées de D' ... mais tout comme pour C', on aura Xd' au signe près.

Il faut alors choisir le bon signe en calculant la longueur C'D' avec le C' qu'on a choisi. Sauf malchance, le signe pour Xd' sera alors imposé.

Puis on recommence avec les points ABE
...

Cela devrait marcher.

:zen:

[Dlzlogic]

Bonjour,
Je me permet d'intervenir dans cette discussion.
D'abord, j'ai été étonné du nombre de décimales dans le fichier de points cité.
Il y a un principe, sauf cas particuliers, 4 points ou plus ne sont jamais coplanaires.
La méthode consiste à trouver un plan qui soit bon, voire très bons, sur lequel on peut projeter l'ensemble des points. Pour différentes raisons, je ne m'étendrai pas sur un synonyme de "bon".
Une fois ce choix fait, il faut vérifier -suivant des critères bien connus- qu'aucun point n'est aberrant (pour quelle que raison que ce soit). Ceci fait, on projette tous les points sur le plan adopté, et si c'est intéressant, on peut calculer les distances de chaque point au plan. Mais, dans tous les cas, sous réserve que la figure est "à peu près plane" on en aura une très bonne représentation.

Pour la pratique du calcul, il me parait important de savoir si la "forme" est toujours la même, je fais référence à un cas où il s'agissait de 25 points répartis suivant un maillage régulier, ou si au contraire la disposition est quelconque.

[sonizef]

J'ai effectivement trouvé ceci :

A' 0,000000000000000 0,000000000000000 0,000000000000000
B' 0,000000000000000 0,597152735161263 0,000000000000000
C' 0,297978669282412 0,535932666517066 0,000000000000000

Mais avec la réserve que Xc' pourrait aussi bien être -0,297978669282412
On prend le signe qu'on veut a priori.

On recommence comme si on avait que les points ABD
Et on trouve par la même méthode les coordonnées de D' ... mais tout comme pour C', on aura Xd' au signe près.

Il faut alors choisir le bon signe en calculant la longueur C'D' avec le C' qu'on a choisi. Sauf malchance, le signe pour Xd' sera alors imposé.

Puis on recommence avec les points ABE
...

Cela devrait marcher.

Donc si j'ai bien compris, il me suffit de "bloquer" les bonnes cellules (les Xa,Ya,Za et Xb,Yb,Zb) puis étendre pour appliquer la formule aux coordonnés du dessous ?

Bonjour,
Je me permet d'intervenir dans cette discussion.
D'abord, j'ai été étonné du nombre de décimales dans le fichier de points cité.
Il y a un principe, sauf cas particuliers, 4 points ou plus ne sont jamais coplanaires.
La méthode consiste à trouver un plan qui soit bon, voire très bons, sur lequel on peut projeter l'ensemble des points. Pour différentes raisons, je ne m'étendrai pas sur un synonyme de "bon".
Une fois ce choix fait, il faut vérifier -suivant des critères bien connus- qu'aucun point n'est aberrant (pour quelle que raison que ce soit). Ceci fait, on projette tous les points sur le plan adopté, et si c'est intéressant, on peut calculer les distances de chaque point au plan. Mais, dans tous les cas, sous réserve que la figure est "à peu près plane" on en aura une très bonne représentation.

Pour la pratique du calcul, il me parait important de savoir si la "forme" est toujours la même, je fais référence à un cas où il s'agissait de 25 points répartis suivant un maillage régulier, ou si au contraire la disposition est quelconque.

Merci de ta réponse, les 25 points sont bien entendu relativement "proche", j'entend par là que plus il y'a de points plus la forme est "complexe". Mais donc en suivant la piste de Black Jack ça devrait fonctionner ?


Merci

[Mathusalem]

Merci de ta réponse, ton idée semble intéressante et plus "automatisable" ..
Seulement voilà j'ai 2 questions :

1) Comment être sur que mes points sont coplanaires ?
2) Est ce que tu pourrai me faire un exemple parce que j'ai un peu de mal à tout saisir :hein:

Si tu a besoin des points de manière concrète pour voir si cela fonctionne, j'ai mis mon tableur avec un avec 3 formes composé de plusieurs points chacune.

Merci pour votre aide.

Pour vérifier que tes points sont bien coplanaires tu prends
1. Tu prends trois points, et tu construis deux vecteurs, par exemple 1-2, que j'appelle , et 1-3 que j'appelle . Par commodité, j'appelle et les mêmes vecteurs mais divisés par leur norme (donc de norme valant 1)

2. Tu construis tous les autres vecteurs 1-4 ,1-5 ,1-6 etc.. Et tu vérifies que


Pour tous les vecteurs c,d,e, etc...

Comme l'a soulevé Dlzlogic, cela ne sera en pratique jamais satisfait à cause de la précision finie de la machine. En revanche, tu peux te donner un intervalle dans lequel tu considères que les points sont suffisamment proche pour être considérés coplanaires : par exemple, si tu retrouves pas exactement à droite de l'égalité (1), tu peux regarder la norme la différence entre la gauche te la droite de l'égalité (1) (qui est censée être une égalité, mais en pratique ne le sera pas) et si par exemple la norme de cette différence est inférieure à un nombre que tu dois estimer, par exemple 0,01, alors tu considère les points comme coplanaires.


Essaye de faire un dessin puis d'implémenter l'algorithme de mon message précédent, ou les autres algorithmes qui te sont proposés.

PS: t'es pas obligé de créer tous les vecteurs comme je le précise la haut. Tu peux prendre simplement les vecteurs que tu as déjà..

[Black Jack]

Autrement :

Coplanaires ou non ?

En partant des données du tableau.

On part de 3 points :

161,81579589843700000 99,48465728759760000 4,31880712509155000
161,23936462402300000 99,36206054687500000 4,41518354415893000
161,37371826171800000 99,20275878906250000 4,63679409027099000

Le plan a pour équation x + ay + bz + c = 0 (sauf dans le cas spécial où tous les 3 points ont une même abscisse x)

on a donc le système :

161,81579589843700000 + 99,48465728759760000.a + 4,31880712509155000.b + c = 0
161,23936462402300000 + 99,36206054687500000.a + 4,41518354415893000.b + c = 0
161,37371826171800000 + 99,20275878906250000.a + 4,63679409027099000.b + c = 0

Facile à résoudre ... mais aussi facile d'être distrait.
On confie donc la résolution à un solver (celui de ma vieille TI:85):

qui donne :
a = -11,9070904614
b = -9,16551181458
c = 1062,34109568

Equation du plan ABC : x - 11,9070904614.y - 9,16551181458.z + 1062,34109568 = 0 ... si je n'ai pas fait trop de fautes en recopiant les chiffres.

Et on remettant les coordonnées des points A , B ... H (de la 1ere série) dans cette équation (presque immédiat par Excel), le membre de gauche de l'équation donne :

0,000000003717 pour le point A
0,000000003751 pour le point B
0,000000003753 pour le point C
-0,000010698577 pour le point D
-0,000004958521 pour le point E
-0,000002563909 pour le point F
0,000005151993 pour le point G
0,000033102192 pour le point H

On ne trouve pas exactement 0 pour les points A, B et C probablement à cause des capacités de calculs de mon solver (ou des erreurs faites en introduisant les nombres dans le solver).

Reste à voir si on peut, avec ces "écarts" calculés (pour les autres points), considérer que les points sont "suffisamment" coplanaires ou non.

:zen:

[sonizef]

Bonjour à tous,
je commence à me mélanger les pinceaux :mur:
Je vous envoi un tableau avec la méthode faite par l'un de vous deux.
J'ai l'impression qu'il y'a une erreur mais quoi :hein:

Tableau ICI

Il me semble que c'était la méthode de Black Jack, mais elle rejoint celle de Mathusalem, non ?

Merci de votre aide

[Black Jack]

Bonjour à tous,
je commence à me mélanger les pinceaux :mur:
Je vous envoi un tableau avec la méthode faite par l'un de vous deux.
J'ai l'impression qu'il y'a une erreur mais quoi :hein:

Tableau ICI

Il me semble que c'était la méthode de Black Jack, mais elle rejoint celle de Mathusalem, non ?

Merci de votre aide

Je n'ai vérifié que le premier groupe (ligne 1 à 8)
Il y a un piège, que j'ai mentionné (signe pour la coordonnées X des points images)
Donc, le "piège" est sur la colonne F (son signe)

Pas de problème pour les points A,B et C, on choisit le signe de Xc (cellule F3) comme on veut.
Mais une fois ce choix fait, il faut prendre garde aux signes pour les cellules F4 à F8.
... Par chance (puisque rien dans tes formules ne le vérifie), ils sont OK (les signes) jusque la cellule F7
Mais le signe est mauvais dans la cellule F8

Pour "corriger" les signes :

Quand on trouve (comme tu l'as fait) le Xd' (cellule F4), on DOIT vérifier quel signe lui attribuer.

Pour se faire, on calcule la longueur CD (par les cellules de B3 à D4)
On calcule la longueur C'D' (à partir de tes cellules F3 à B4)
Si on trouve CD = C'D' ... c'est que le signe mis pour la valeur dans la cellule F4 est bon.
Si on n'a pas CD = C'D', c'est que le signe mis pour la valeur dans la cellule F4 est mauvais et il faut le changer.

Et cela fait, on recommence pour les lignes suivantes.
on calcule la longueur DE (par les cellules de B4 à D5)
On calcule la longueur D'E' (à partir des cellules F4 à B5)
Si on trouve DE = D'E' ... c'est que le signe mis pour la valeur dans la cellule F5 est bon.
Si on n'a pas DE = D'E', c'est que le signe mis pour la valeur dans la cellule F5 est mauvais et il faut le changer.

...

Si on fait cela pour tout le premier groupe, tu as le bon signe partout dans ta colonne F ... sauf pour la cellule F8 qui a le mauvais signe.
*****

Il manque donc un "test" à chaque cellule F à partir de F4 (jusque la F8) pour "choisir" le bon signe pour ces cellules.

Attention que si tu tentes d'implémenter ce test, qu'il faut prendre les précautions d'usage pour comparer des résultats de calculs en float.
Tester une égalité avec des floats est périlleux, il vaut mieux tester le rapport |CD|/|C'D'| et de décider l'égalité si ce rapport est compris entre 0,99 et 1,01 (par exemple) plutôt que d'écrire un très risqué "Si CD = C'D' ..."


:zen: