Bonjour , je ne comprend vraiment rien à ces théorèmes , je ne sais comment les utiliser et je viens demander votre aide ...
Soit p(x) = 2x^4 + 3x^3 - 3x^2 +3x + 2
1) donner la borne de Cauchy M
2) à l'aide du théorème de Sturm , montrer que p(x) a 2 racines réelles
Merci d'avance de votre aide ..
Cauchy et Sturm
8 messages
- Page 1 sur 1
D'accord, on te demande en exercice d'expliciter la borne de Cauchy pour un polynôme sans t'avoir expliqué en cours ce qu'est la borne de Cauchy.
Tu peux m'expliquer cette situation ? Parce que j'avoue que j'ai un peu de mal à comprendre.
Pareil sans doute, on te demande d'appliquer le théorème de Sturm sans t'avoir expliqué ce que c'est ?
Tu peux m'expliquer cette situation ? Parce que j'avoue que j'ai un peu de mal à comprendre.
Pareil sans doute, on te demande d'appliquer le théorème de Sturm sans t'avoir expliqué ce que c'est ?
Le signe "moins" devant la dérivée de 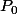 ne devrait pas y être. Un extrait de résumé de cours que j'avais écrit dans le temps :
ne devrait pas y être. Un extrait de résumé de cours que j'avais écrit dans le temps :
Soit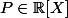 . La suite de Sturm de
. La suite de Sturm de  est la suite de polynômes obtenus dans l'algorithme d'Euclide pour la recherche du pgcd de
est la suite de polynômes obtenus dans l'algorithme d'Euclide pour la recherche du pgcd de  et de son polynôme dérivé
et de son polynôme dérivé 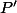 , à ceci près que l'on prend à chaque fois l'opposé du reste de la division euclidienne, au lieu de prendre le reste:
, à ceci près que l'on prend à chaque fois l'opposé du reste de la division euclidienne, au lieu de prendre le reste:
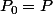 ,
,  ,
,  l'opposé du reste de la division euclidienne de
l'opposé du reste de la division euclidienne de  par
par 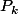 pour
pour 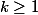 ,
,  le dernier polynôme non nul obtenu (un pgcd de
le dernier polynôme non nul obtenu (un pgcd de  et
et 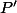 ).
).
Si n'est pas une racine de
n'est pas une racine de  , on pose
, on pose  =) le nombre de changements de signe dans la suite des valeurs
le nombre de changements de signe dans la suite des valeurs ,P_1(a),\ldots,P_N(a)) . On compte un changement de signe quand
. On compte un changement de signe quand P_{k+1}(a)<0) , ou quand
, ou quand P_{k+\ell}(a)<0) et que
et que =\ldots=P_{k+\ell-1}(a)=0) .
.
Théorème de Sturm
Soient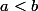 deux nombres réels qui ne sont pas racines de
deux nombres réels qui ne sont pas racines de  . Alors le nombre de racines réelles distinctes de
. Alors le nombre de racines réelles distinctes de  dans
dans 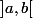 est égal à
est égal à -v_P(b)) .
.
Exemple: la suite de Sturm de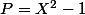 est
est 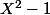 ,
,  ,
,  . On a
. On a =2) ,
, =1) ,
, =0) . On sait bien qu'il y a une racine de
. On sait bien qu'il y a une racine de  dans
dans  et une dans
et une dans 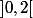 .
.
Soit
Si
Théorème de Sturm
Soient
Exemple: la suite de Sturm de
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
