Sturm-Liouville
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 09 Fév 2012, 12:45
par Pythales » 09 Fév 2012, 12:45
Bonjour à tous
voici l'énoncé sur lequel je travaille :
,\ q(x)\ et\ y(x))
sont trois fonctions

et

vérifie l'équation

Si
)
n'est pas identiquement nulle, montrer que :
1)

ne s'annulent pas simultanément
2) Les zéros de

sont en nombre fini.
Je pense avoir la solution du 1) (encore que...je m'en expliquerai). Pour le 2) je cherche encore.
Merci de me donner quelques pistes.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 09 Fév 2012, 13:27
par Doraki » 09 Fév 2012, 13:27
Ben la 1 est dure, alors que la 2, ben on suppose qu'il y a une infinité de zéros, et on en déduit qu'il existe un point qui annule y et y', ce qui contredit le 1.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 09 Fév 2012, 16:49
par Pythales » 09 Fév 2012, 16:49
Doraki a écrit:Ben la 1 est dure, alors que la 2, ben on suppose qu'il y a une infinité de zéros, et on en déduit qu'il existe un point qui annule y et y', ce qui contredit le 1.
Les zéros sont en nombre
fini

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 09 Fév 2012, 17:37
par raito123 » 09 Fév 2012, 17:37
Bonjour,
Pythales a écrit:Les zéros sont en nombre fini
Doraki le sait très bien ... il a justement fait un raisonnement par absurde !!
Et puis pour la première question c'est pas vraiment dure ... c'est juste une conséquence de la condition de Cauchy-Lipschitz ( en utilisant toujours un raisonnement par absurde )
Les multiples ne doivent pas être utilisés sans nécessité
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 09 Fév 2012, 17:45
par Doraki » 09 Fév 2012, 17:45
raito123 a écrit:c'est juste une conséquence de la condition de Cauchy-Lipschitz ( en utilisant toujours un raisonnement par absurde )
Ah ben peut-être. C'est pas tellement mon domaine de prédilection alors j'ai oublié tous ces trucs depuis le temps.

-
raito123
- Habitué(e)
- Messages: 2102
- Enregistré le: 04 Nov 2007, 02:29
-
 par raito123 » 09 Fév 2012, 17:58
par raito123 » 09 Fév 2012, 17:58
Doraki a écrit:Ah ben peut-être. C'est pas tellement mon domaine de prédilection alors j'ai oublié tous ces trucs depuis le temps.
Si je puis me permettre ton niveau est trop bien


Sinn pour la première question vu que les fcts p et q sont de classe C2 alors le système différentiel vérifie le condition de Cauchy-Lip et donc comme la fonction nulle est solution du système elle serait l'unique solution qui s'annule elle et sa dérivée première en un point !!
Les multiples ne doivent pas être utilisés sans nécessité
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 09 Fév 2012, 18:43
par Pythales » 09 Fév 2012, 18:43
OK. Merci. Pour la 1, c'est vrai que c'est évident par le théorème.
Par contre, pourquoi peut-on dire que y et y' s'annuleraient simultanément si les zéros n'étaient pas en nombre fini ?
-
Arkhnor
- Membre Relatif
- Messages: 343
- Enregistré le: 05 Déc 2008, 20:02
-
 par Arkhnor » 09 Fév 2012, 20:28
par Arkhnor » 09 Fév 2012, 20:28
Bonsoir,
Considère un point d'accumulation de ces zéros. (on est dans un compact)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 09 Fév 2012, 21:41
par Pythales » 09 Fév 2012, 21:41
Arkhnor a écrit:Bonsoir,
Considère un point d'accumulation de ces zéros. (on est dans un compact)
C'est bien ce à quoi je pense, mais sur quel théorème s'appuyer ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 09 Fév 2012, 21:43
par Doraki » 09 Fév 2012, 21:43
Ben une suite et un compact, ça devrait te hurler "bolzano-weierstrass".
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 09 Fév 2012, 22:00
par Pythales » 09 Fév 2012, 22:00
Doraki a écrit:Ben une suite et un compact, ça devrait te hurler "bolzano-weierstrass".
Je connais Bolzano-Weierstrass (tout ensemble fermé ayant ...), mais quel rapport avec lla dérivée ?
-
Arkhnor
- Membre Relatif
- Messages: 343
- Enregistré le: 05 Déc 2008, 20:02
-
 par Arkhnor » 09 Fév 2012, 22:20
par Arkhnor » 09 Fév 2012, 22:20
Montre que la dérivée est nulle au point d'accumulation. (la fonction prend une infinité de fois la même valeur au voisinage de ce point, ça te permet par Rolle de construire aussi une suite de zéros de la dérivée qui converge vers le point en question)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 10 Fév 2012, 10:11
par Pythales » 10 Fév 2012, 10:11
Arkhnor a écrit:Montre que la dérivée est nulle au point d'accumulation. (la fonction prend une infinité de fois la même valeur au voisinage de ce point, ça te permet par Rolle de construire aussi une suite de zéros de la dérivée qui converge vers le point en question)
OK.Merci.
Je pensais qu'il y avait un théorème que j'ignorais.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Fév 2012, 11:26
par Doraki » 10 Fév 2012, 11:26
T'as pas besoin de Rolle du tout, si t'appelles a un point d'accumulation de l'ensemble des zéros de y,
t'as juste besoin de la définition de "dérivée de y en a" comme limite du taux d'accroissement.
Comme c'est une limite qui existe d'un truc qui prend la valeur 0 autant de fois que tu veux dans n'importe quel intervalle autour de a, ça ne peut être que 0.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 10 Fév 2012, 11:29
par Pythales » 10 Fév 2012, 11:29
J'ai dit que je pensais avoir la solution de 1) :
Si
=y'(x_0)=0)
, en dérivant l'équation, on montre que
}(x_0)=0\forall n)
, et le développement de

en série montre que

est la fonction nulle.
Mais j'ai ensuite pensé à la fonction

dont le développement en série autour de 0 est nul, et qui n'est pourtant pas nulle pour
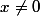
Comment expliquer cette différence, sachant que ladite fonction est bien

?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 10 Fév 2012, 11:39
par Pythales » 10 Fév 2012, 11:39
Cela dit, je ne suis (certainement à tort), qu'à moitié convaincu, car lorsqu'on s'approche du point d'accumulation, dx tend vers 0, mais dy tend aussi vers 0, de sorte que le rapport dy/dx est indéterminé.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Fév 2012, 11:44
par Doraki » 10 Fév 2012, 11:44
Pythales a écrit:J'ai dit que je pensais avoir la solution de 1) :
Si
=y'(x_0)=0)
, en dérivant l'équation, on montre que
}(x_0)=0\forall n)
, et le développement de

en série montre que

est la fonction nulle.
Mais j'ai ensuite pensé à la fonction

dont le développement en série autour de 0 est nul, et qui n'est pourtant pas nulle pour
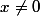
Comment expliquer cette différence, sachant que ladite fonction est bien

?
Ce n'est pas une preuve du 1. C'est Cauchy-Lipschitz qui est attendu ici.
Et y(x) = e^-1/x² n'est pas un contre-exemple parceque tu ne peux pas trouver de fonctions p et q bien définies tel que y"+py'+qy = 0 (y" tend trop lentement vers 0 comparé à y et y').
Cela dit, je ne suis (certainement à tort), qu'à moitié convaincu, car lorsqu'on s'approche du point d'accumulation, dx tend vers 0, mais dy tend aussi vers 0, de sorte que le rapport dy/dx est indéterminé.
Tu parles de quoi là ?
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 10 Fév 2012, 12:53
par Pythales » 10 Fév 2012, 12:53
Doraki a écrit:Ce n'est pas une preuve du 1. C'est Cauchy-Lipschitz qui est attendu ici.
Et y(x) = e^-1/x² n'est pas un contre-exemple parceque tu ne peux pas trouver de fonctions p et q bien définies tel que y"+py'+qy = 0 (y" tend trop lentement vers 0 comparé à y et y').
Tu parles de quoi là ?
Je parle de la preuve que y'=0 au point d'accumulation
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 10 Fév 2012, 13:26
par Doraki » 10 Fév 2012, 13:26
Ben 0, c'est 0, ce n'est pas un truc qui tend vers 0.
0/(x-a), ça fait encore 0.
Tu as un truc qui a une limite en a et qui passe par 0 autant de fois que tu veux dans n'importe quel voisinage de a.
La limite ne peut être que 0.
On peut simplifier la preuve en réduisant Bolzano-weierstrass :
Soit a tel que y(a) = 0. Alors il existe un ouvert U(a) contenant a tel que a est le seul zéro de y dans U(a) :
En effet, y'(a) est non nul d'après 1.
Donc (définition de dérivée), la limite quand x tend vers a de y(x)/(x-a) est non nulle.
Donc (définition de limite), comme R* est un ouvert contenant la limite en question, il existe un ouvert U(a) contenant a tel que pour tout x de U(a)\{a}, y(x)/(x-a) est non nul.
Et donc pour tout x de U(a)\{a}, y(x) est non nul.
Maintenant, [0;1] = la réunion de l'image réciproque de R* par y et des U(a) pour tous les a tels que y(a)=0.
En effet, si x est dans [0;1], ou bien y(x)=0 et alors x est dans U(x) ; ou bien y(x) est non nul et alors x est dans l'image réciproque de R* par y.
C'est un recouvrement de [0;1] par des ouverts (R* est un ouvert et y est continue, donc l'image réciproque de R* par y est un ouvert)
Comme [0;1] est compact, on en extrait un recouvrement fini.
Pour tout a tel que y(a) = 0, U(a) était le seul ouvert du recouvrement qui contienne a, donc le recouvrement fini doit contenir U(a).
Donc il y a un nombre fini de U(a), donc y a un nombre fini de zéros.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 10 Fév 2012, 13:51
par Pythales » 10 Fév 2012, 13:51
Doraki a écrit:Ben 0, c'est 0, ce n'est pas un truc qui tend vers 0.
0/(x-a), ça fait encore 0.
Tu as un truc qui a une limite en a et qui passe par 0 autant de fois que tu veux dans n'importe quel voisinage de a.
La limite ne peut être que 0.
On peut simplifier la preuve en réduisant Bolzano-weierstrass :
Soit a tel que y(a) = 0. Alors il existe un ouvert U(a) contenant a tel que a est le seul zéro de y dans U(a) :
En effet, y'(a) est non nul d'après 1.
Donc (définition de dérivée), la limite quand x tend vers a de y(x)/(x-a) est non nulle.
Donc (définition de limite), comme R* est un ouvert contenant la limite en question, il existe un ouvert U(a) contenant a tel que pour tout x de U(a)\{a}, y(x)/(x-a) est non nul.
Et donc pour tout x de U(a)\{a}, y(x) est non nul.
Maintenant, [0;1] = la réunion de l'image réciproque de R* par y et des U(a) pour tous les a tels que y(a)=0.
En effet, si x est dans [0;1], ou bien y(x)=0 et alors x est dans U(x) ; ou bien y(x) est non nul et alors x est dans l'image réciproque de R* par y.
C'est un recouvrement de [0;1] par des ouverts (R* est un ouvert et y est continue, donc l'image réciproque de R* par y est un ouvert)
Comme [0;1] est compact, on en extrait un recouvrement fini.
Pour tout a tel que y(a) = 0, U(a) était le seul ouvert du recouvrement qui contienne a, donc le recouvrement fini doit contenir U(a).
Donc il y a un nombre fini de U(a), donc y a un nombre fini de zéros.
Merci. Je vais regarder ça à tête reposée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
, en dérivant l'équation, on montre que
, et le développement de
en série montre que
est la fonction nulle.
dont le développement en série autour de 0 est nul, et qui n'est pourtant pas nulle pour
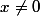
?