Bonjour, comment montrer que (A u B) est un ensemble fini en utilisant le Card(A) et Card(B) à l'aide de la définition? (1)
Et aussi, comment montrer que Card((A u B)) = Card(A) + Card(B) - Card(A n B) à l'aide de la définition ? (2)
Voilà la définition :
On dit que E est un ensemble fini s'il existe un unique entier naturel n et f une bijection de {1,2,..,n} dans E.
On appelle n le cardinal de E et on le note Card(E)
Voilà ce que j'ai écrit :
(AuB) est l'ensemble des éléments de A et de B. Or A et B sont finis donc A u B est fini.
Cette explication n'est pas très mathématique est trop paraphrasée je trouve, quel est la bonne facon de le dire ?
Ensuite : (Quand je parle d'un ensemble ici je parle de son cardinal)
AuB est l'ensemble des éléments de A et de B. Cependant, AuB n'admet aucun doublon, c'est pour cela qu'on soustrait AnB.
De même pour le dessus, c'est trop abstrait et paraphrasée et pas assez mathématique.
J'aimerais avoir vos proposition de réponse a ces questions ou bien des avis ou indications. Je n'arrive pas a utiliser des quantificateurs pour ces exos.
Merci bcp!
Cardinalité et ensembles finis
6 messages
- Page 1 sur 1
Re: Cardinalité et ensembles finis
On va tout d'abord supposer 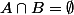 , le cas général s'en déduira facilement. Pour montrer que
, le cas général s'en déduira facilement. Pour montrer que 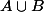 est fini, il faut exhiber un entier
est fini, il faut exhiber un entier  et une bijection de
et une bijection de 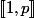 dans
dans 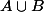 . On s'en doute
. On s'en doute 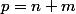 puisque c'est censé être le cardinal de
puisque c'est censé être le cardinal de 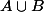 . Si
. Si  (resp
(resp  ) est une bijection de
) est une bijection de 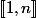 (resp
(resp  ) dans
) dans  (resp
(resp  ), on définit
), on définit  par :
par :
=f(k))
=g(k-n))
Il est assez clair que c'est une bijection : si=h(k')) alors comme
alors comme 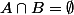 ,
, =h(k')) est ou bien dans
est ou bien dans  ou bien dans
ou bien dans  , ainsi
, ainsi 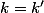 par injectivité de
par injectivité de  ou
ou  selon le cas, la surjectivité se traite de la même manière. Bref
selon le cas, la surjectivité se traite de la même manière. Bref  est une bijection donc
est une bijection donc 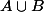 est fini et de cardinal
est fini et de cardinal +\mathrm{Card}(B)) . Revenons au cas général, si on prend
. Revenons au cas général, si on prend  et
et  quelconques, posons
quelconques, posons  alors
alors  et
et  donc d'après ce qui précède,
donc d'après ce qui précède,  est fini et
est fini et =\mathrm{Card}(A'\cup B)=\mathrm{Card}(A')+\mathrm{Card}(B)) . D'autre part,
. D'autre part, =A) et puisque
et puisque =\emptyset) alors d'après le premier point,
alors d'après le premier point, =\mathrm{Card}(A')+\mathrm{Card}(A\cap B)) d'où
d'où =\mathrm{Card}(A)-\mathrm{Card}(A\cap B)) puis enfin
puis enfin =\mathrm{Card}(A)+\mathrm{Card}(B)-\mathrm{Card}(A\cap B)) (ouf !).
(ouf !).
Il est assez clair que c'est une bijection : si
Re: Cardinalité et ensembles finis
@Kugge Ce que tu as écrit n'est effectivement pas une démonstration mathématique.
Pour démontrer que AUB est fini, il suffit ... de vérifier la définition.
Premier cas : A et B en union disjointe.
On construit une bijection de {1,...,card(A)+card(B)} dans AUB (l'union est disjointe)
On généralise aisément par récurrence que si A1, A2, ..., Ak sont finis, l'union disjointe
A1UA2U...UAk est finie, et de cardinal card(A1)+...+card(Ak).
Cas général : on écrit AUB = (A\B)U(A inter B) U (B/A), l'union étant disjointe dans le membre de droite.
Et on applique le résultat précédent à cette union disjointe.
Conclusion : AUB est fini et card(AUB) = card(A\B) + card(A inter B) + card(B\A).
On conclut aisément encore une fois en justifiant que card(A\B) = card(A) - card(A inter B) par union disjointe.
Je ne sais pas s'il existe une démonstration plus simple, ou si les autres démonstrations reviennent à ce que j'ai fait ici.
@Tuvasbien : nos messages se sont croisés! Dans ton message, tu explicites la construction rigoureuse de la bijection évoquée, dans le cas A et B disjoints. C'est la clé de la démonstration
@Kugge : en général en combinatoire, pour montrer que deux ensembles ont même cardinal, on peut chercher une preuve bijective, c'est à dire à construire une bijection d'un ensemble vers l'autre. Cela peut être assez compliqué d'avoir l'idée d'une telle bijection (la combinatoire est parfois une affaire de spécialiste)
Pour démontrer que AUB est fini, il suffit ... de vérifier la définition.
Premier cas : A et B en union disjointe.
On construit une bijection de {1,...,card(A)+card(B)} dans AUB (l'union est disjointe)
On généralise aisément par récurrence que si A1, A2, ..., Ak sont finis, l'union disjointe
A1UA2U...UAk est finie, et de cardinal card(A1)+...+card(Ak).
Cas général : on écrit AUB = (A\B)U(A inter B) U (B/A), l'union étant disjointe dans le membre de droite.
Et on applique le résultat précédent à cette union disjointe.
Conclusion : AUB est fini et card(AUB) = card(A\B) + card(A inter B) + card(B\A).
On conclut aisément encore une fois en justifiant que card(A\B) = card(A) - card(A inter B) par union disjointe.
Je ne sais pas s'il existe une démonstration plus simple, ou si les autres démonstrations reviennent à ce que j'ai fait ici.
@Tuvasbien : nos messages se sont croisés! Dans ton message, tu explicites la construction rigoureuse de la bijection évoquée, dans le cas A et B disjoints. C'est la clé de la démonstration
@Kugge : en général en combinatoire, pour montrer que deux ensembles ont même cardinal, on peut chercher une preuve bijective, c'est à dire à construire une bijection d'un ensemble vers l'autre. Cela peut être assez compliqué d'avoir l'idée d'une telle bijection (la combinatoire est parfois une affaire de spécialiste)
Modifié en dernier par LB2 le 06 Oct 2019, 23:35, modifié 1 fois.
Re: Cardinalité et ensembles finis
Pour la première question, on te dit : 'monter que A U B est un ensemble fini en utilisant Card(A) et Card(B).
Et dans ta réponse , tu n'emploie à aucun moment le mot 'Cardinal'. Ta réponse n'est donc pas celle attendue.
Et pour la 2ème question .... j'aime encore moins ta réponse.
Edit : 2 réponses ont été postées pendant que j'écrivais... tant pis si ça fait doublon.
Et dans ta réponse , tu n'emploie à aucun moment le mot 'Cardinal'. Ta réponse n'est donc pas celle attendue.
Et pour la 2ème question .... j'aime encore moins ta réponse.
Edit : 2 réponses ont été postées pendant que j'écrivais... tant pis si ça fait doublon.
Re: Cardinalité et ensembles finis
lyceen95, je ne sais pas si tu t'adresses à moi ou à Tuvasbien, mais il me semble que s'il y a un problème de rigueur, il se situe davantage dans l'énoncé exact de la question : "comment montrer que (A u B) est un ensemble fini en utilisant le Card(A) et Card(B) à l'aide de la définition?"
n'est pas très bien formulé, il faudrait dire plus simplement: "comment montrer que (A u B) est un ensemble fini à l'aide de la définition?".
n'est pas très bien formulé, il faudrait dire plus simplement: "comment montrer que (A u B) est un ensemble fini à l'aide de la définition?".
Re: Cardinalité et ensembles finis
Je m'adressais à Kugge ; je n'avais pas vu vos messages quand j'ai envoyé le mien.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
