Bijection équation d'ensemble cardinalité

[abicah]

Bonjour ,

Quelqu'un peut-t-il me confirmer que la bijection de la solution de la question 2 (en rouge) de l'exercice suivant https://ibb.co/BTskrNx est mal définie ?

Merci

[tournesol]

J'aurais écrit: X donne

[Ben314]

Salut,

J'aurais écrit: X donne

J'ai un peu des doutes du fait que si veut avoir des chances que , ben vaudrait mieux qu'on ait , non ?
Perso., je prendrais soit , soit (avec toujours )

[abicah]

Salut,

J'aurais écrit: X donne

J'ai un peu des doutes du fait que si veut avoir des chances que , ben vaudrait mieux qu'on ait , non ?
Perso., je prendrais soit , soit (avec toujours )

Effectivement C'est bien la réponse que j'attendais merci à tous les deux

[abicah]

Pardon pour le B n X barre j 'ai un doute il faut que je regarde, par contre pour le (A barre n B ) u X je suis sur...

[abicah]

Salut,

J'aurais écrit: X donne

J'ai un peu des doutes du fait que si veut avoir des chances que , ben vaudrait mieux qu'on ait , non ?
Perso., je prendrais soit , soit (avec toujours )

Effectivement C'est bien la réponse que j'attendais merci à tous les deux

Je confirme ca m'a l 'air tout bon

Merci bien

[tournesol]

Désolé j'ai du me tromper mais voici ce que j'aurais fait:
ssi
On utilise la question précédente
Si c'est à dire si , pas de solution.
Si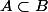 alors le cardinal est celui de , soit

[abicah]

Désolé j'ai du me tromper mais voici ce que j'aurais fait:
ssi
On utilise la question précédente
Si c'est à dire si , pas de solution.
Si alors le cardinal est celui de , soit

Effectivement ta solution est plus élégante que celle de l 'exercice, elle exploite entièrement le résultat de la question précédente et évite ainsi dé redéfinir une bijection

Merci

[abicah]

Désolé j'ai du me tromper mais voici ce que j'aurais fait:
ssi
On utilise la question précédente
Si c'est à dire si , pas de solution.
Si alors le cardinal est celui de , soit

Bonjour,

Finalement, j'ai un doute sur la manière dont tu t 'y prends pour aboutir au résultat , car tu raisonnes
comme si les 2 équations étaient du même "type" alors qu'il y en une qui est en "X" et la seconde en "X barre"
elles ne sont donc pas vraiment superposables et au final tu fait le calcul des "X barres" et non celui des "X"
comme demandé

[Ben314]

Oui, mais l'application de dans lui même est clairement bijective (c'est même une involution, c'est à dire que sa bijection réciproque c'est elle même).
Donc compter combien il y a de tels que . . . ou bien combien il y a de 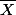tels que . . ., c'est la même chose.

[abicah]

Oui, mais l'application de dans lui même est clairement bijective (c'est même une involution, c'est à dire que sa bijection réciproque c'est elle même).
Donc compter combien il y a de tels que . . . ou bien combien il y a de tels que . . ., c'est la même chose.

Donc au final on est quand même obligé de passer par une bijection pour déduire le résultat même si dans ce cas elle est implicite

[Ben314]

Sur le principe, oui, sauf que le fait que de dans lui soit une bijection est tellement une "évidence évidente" que l'on omet régulièrement de le préciser.

Par exemple là, je suis sûr à 100% que, pour tournesol, de compter les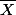 solutions c'était bien la même chose que de compter les solutions. Et s'il ne l'a pas écrit explicitement, c'est du fait que ça lui semblait évident.

[abicah]

Sur le principe, oui, sauf que le fait que de dans lui soit une bijection est tellement une "évidence évidente" que l'on omet régulièrement de le préciser.

Par exemple là, je suis sûr à 100% que, pour tournesol, de compter les solutions c'était bien la même chose que de compter les solutions. Et s'il ne l'a pas écrit explicitement, c'est du fait que ça lui semblait évident.

On aurait pu aussi dire que la restriction à S (l'ensemble des X barre vérifiant l 'équation) de l'involution f que tu viens d'exhiber est aussi bijective de S sur f(S) (l'ensemble des X vérifiant l'équation) et donc que |S|=|f(S)|

[Ben314]

Oui, mais le fait que, si on a une bijection f de E dans F, alors pour toute partie A de E, la restriction de f à A est une bijection de A sur f(A) est de nouveau suffisamment évident pour que pas mal d'auteurs l'utilisent sans rien dire.
Mais bien évidement, tout dépend du "bagage" que l'on a et je trouve ça on ne peut plus sain que tu te pose les questions que tu te pose (sauf que, d'ici peu, tu fera comme tout le monde, à savoir trouver ça suffisamment évident pour que ce soit même pas la peine d'en parler . . .)

[abicah]

Oui, mais le fait que, si on a une bijection f de E dans F, alors pour toute partie A de E, la restriction de f à A est une bijection de A sur f(A) est de nouveau suffisamment évident pour que pas mal d'auteurs l'utilisent sans rien dire.
Mais bien évidement, tout dépend du "bagage" que l'on a et je trouve ça on ne peut plus sain que tu te pose les questions que tu te pose (sauf que, d'ici peu, tu fera comme tout le monde, à savoir trouver ça suffisamment évident pour que ce soit même pas la peine d'en parler . . .)

En tout les cas merci pour ta contribution

[tournesol]

Bonjour à tous
Oui Ben314 , j'ai bien considéré que X donne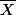 est bijective sur P(E).
Je rappelle pourquoi une involution est bijective sur son ensemble de définition:
soit f une application de E dans F , et g une application de F dans G
alors gof injective implique f injective , et gof surjective implique g surjective.
J'essairai de répondre dans la journée sur l'équation qui nous interresse .

[tournesol]

Voici une généralisation de ma méthode.
On donne:
un ensemble non vide E et G et H des parties non vide de ,
et f une application de E dans E .
Pour tout (a,b) appartenant à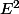 on pose
et
On suppose que pour tout (x,a,b) appartenant à
ssi ( ssi )
Cet équivalence veut dire que et que
f induit donc une application de dans
Supposons f injective ; alors toute restriction de f l'est ; en particulier
Supposons f surjective et soit y appartenant à
est non vide (car f est surjective) , et inclus dans
Donc est surjective .
En particulier, si f est bijective alors l'est aussi et les ensembles et sont équipotents.