Cardinal d'une classe d'équivalence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Jeejsaas
- Membre Naturel
- Messages: 10
- Enregistré le: 17 Oct 2018, 13:32
-
 par Jeejsaas » 16 Jan 2019, 13:06
par Jeejsaas » 16 Jan 2019, 13:06
Bonjour, j'ai un doute sur une question sur les classes d'équivalence et je souhaiterais savoir si mon raisonnement est juste
Soit
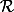
une relation d'équivalence sur
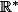
définie par
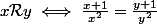
On voit donc que
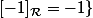

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Jan 2019, 14:00
par Ben314 » 16 Jan 2019, 14:00
Salut,
Ce n'est pas
UNE (article
indéfini) relation d'équivalence définie par . . . mais
LA (article
défini) relation d'équivalence définie par . . .
(c'est on ne peut plus important en math de distinguer les articles définis de ceux indéfinis)^2}\!=\!\dfrac{x\!+\!1}{x^2}\Leftrightarrow x\!=\!-1)
Ce qui signifie que la classe du réel

pour la relation
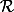
est l'ensemble
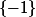
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités