Calculer Acos(x) sans la fonction Acos

[Anonyme]

Bonjour

Je cherche à calculer Acos(x) avec un logiciel qui ne dispose pas des fonctions Acos et Asin, mais seulement de cos, sin, tan et Atan. Comment faire ?

Merci d'avance pour votre réponse.

[Black Jack]

Arccos(x) = Pi + Arctan(V(1-x²) / x) si x est compris dans [-1 ; 0[
Arccos(x) = Arctg(V(1-x²) / x) si x est compris dans ]0 ; 1]

Arccos(x) = +/- Pi/2 si x = 0
@@@@@@@

Démo :
Arccos(x) = y
cos(y) = x
Si x est dans ]0 ; 1], alors sin(x) = V(1 - x²)
tg(y) = V(1-x²) /x
y = Arctg(V(1-x²) /x)
Et donc : Arccos(x) = Arctg(V(1-x²) /x)

Je te laisse faire l'exercice pour x compris dans [-1 ; 0[
...

:zen:

[Anonyme]

Merci Black Jack pour ta réponse.

Le logiciel en question utilise le VBScript et avec quelques recherches plus poussées sur la toile j'ai trouvé la fonction :

function Acos(a) en VBScript
if Abs(a)=1 then Acos = (1-a)*PI/2
else Acos = Atn(-a/Sqr(1-a*a))+2*Atn(1)
end function

Mais pour l'instant je ne sais pas comment je vais pouvoir la mettre dans ma formule pour calculer la surface mouillée d'une canalisation :
Sm = R^2*Acos((R-h)/R)-(R-h)*Sqr(R^2-(R-h)^2)
avec Sm en m², R le rayon en m et h la hauteur d'eau dans la conduite en m.
:marteau:
Tous cela pour calculer le débit dans une conduite :
Q = Sm*V
avec Q le débit en m3/s et V la vitesse en m/s.

[mathelot]

Bonjour 4nt0 (ça faisait un bail!),


on peut écrire la routine suivante pour obtenir une valeur
approchée d'arccos(u):

quand u est négatif , , c'est à dire


ce qui permet de ne traiter que des arguments positifs , dans


calculons
est donné , en entrée de la routine, il s'agit de calculer une valeur approchée de :


x est donc racine de l'équation:


on trouve d'excellentes valeurs approchées en considérant
la formule de récurrence (méthode de Newton-Raphson de résolution de l' équation f(x)=0)




la valeur initiale peut valoir:
si
si

PS: pour , prendre la valeur approchée

qui doit donner 14 décimales exactes

[mathelot]

bonjour,

j'ai ecrit un petit prog sur ma TI89, qui donne de bons résultats:
je ne sais si tu as la possibilité d'implémenter une boucle de programmation.

calcul_acos()

' valeur approchée de pi à 14 décimales
->



'l'argument en entrée:

Input u

' pour les valeurs négatives

0 -> top
if (u
1 -> top
endif



' i est un compteur de boucle
0 -> i


if (u>0,5) then
' valeur initiale de la suite pour les grands cosinus
->
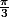else
' valeur initiale de la suite pour les petits cosinus
->
endif

while i
->
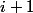endwhile

' renvoie arccos(u)
if (top=0) then
Disp
else
Disp
endif
return

----------------------tests ------------------
Pour les valeurs remarquables de u, u>0
x=1,04719755120
x=785348163397
x=0,523548775599
x=0,314159265359

le prog renvoie x=arccos(u) avec 10 décimales exactes.

[mathelot]

formule pour calculer la surface mouillée d'une canalisation :


valide pour

[Anonyme]

Bonjour mathelot

C'est vrai que ça fait un bail et je suis tjrs avec mes problèmes de surface mouillée, mais maintenant que j'ai les bonnes formules je ne peux pas les appliquer dans mon progiciel car il ne connaît pas l'Arcos.
Bref je vais me renseigner auprès du constructeur pour savoir si je peux mettre dans la partie calcul ton petit programme.

pour info : le logiciel que j'utilise s'appel EMMA (progiciel de traitement des mesures de l’autosurveillance des réseaux d'assainissement)

ps : ta formule de surface mouillée est juste aussi

[mathelot]

je ne peux pas les appliquer dans mon progiciel car il ne connaît pas l'Arcos.

idée: s'inspirer de l'algorithme CORDIC (calcul effectif d'un cos
par les calculatrices) pour trouver un algorithme
similaire pour arccos.
je vais regarder ça ce soir.

L'année dernière, j'avais un projet qui me tenait à coeur, c'était d'obtenir
des formules de surface mouillée pratiques pour des conduits de section elliptique. Il faut que je retrouve nos écrits d'alors.
es-tu tjrs intéressé ?