Bonjour,
Wolfram me donne une formule que je n’arrive pas à trouver pour cette inégrale. Merci de m’aider.
Il s’agit de l’intégrale de racine(cosx) /( 1+cosx) entre 0 et pi/2 .
Au fait on demandait juste de prouver qu’elle est >ln2 dans l’énoncé,
Calcul d’une intégrale
4 messages
- Page 1 sur 1
Re: Calcul d’une intégrale
Hello,
Tu peux commencer par utiliser au numérateur l'inégalité\geq \sin(x)) vraie sur l'intervalle d'intégration. Ensuite, tu peux composer avec
vraie sur l'intervalle d'intégration. Ensuite, tu peux composer avec 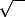 et te rappeler que
et te rappeler que 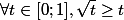 . Tu devrais voir apparaître une fonction de la forme
. Tu devrais voir apparaître une fonction de la forme 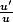 dans ton intégrale.
dans ton intégrale.
Tu peux commencer par utiliser au numérateur l'inégalité
Re: Calcul d’une intégrale
Hummm.... J'ai un peu des doutes concernant le fait que \!\geqslant\sin(x)) . . .
. . .
En passant par l'arc moitié, on voit que l'intégrale c'est l'aire du domaine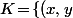\!\in\!{\mathbb R}_+^2\mbox{ t.q. }(1\!+\!x^2)(1\!+\!y^2)\!\leqslant\!2\}) .
.
Mais je sais pas trop quoi faire ensuite . . .
En passant par l'arc moitié, on voit que l'intégrale c'est l'aire du domaine
Mais je sais pas trop quoi faire ensuite . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Calcul d’une intégrale
Ben314 a écrit:Hummm.... J'ai un peu des doutes concernant le fait que. . .
Oups... dans ma tête on allait jusqu'à
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
