Calcul de la somme d'une série
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 05 Mai 2021, 09:36
par Frandom94 » 05 Mai 2021, 09:36
Bonjour tout le monde,
Je bloque sur un problème sans doute très simple. Je dois calculer la somme de la série suivante :
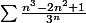
Merci d'avance pour votre aide !

-
alanbry75
- Messages: 5
- Enregistré le: 04 Mai 2021, 14:03
-
 par alanbry75 » 05 Mai 2021, 11:40
par alanbry75 » 05 Mai 2021, 11:40
il doit etre plus simple de calculer
x^n=x^2\sum (n-1)(n^2-n-1)x^{n-2}=x^2(\sum (n^2-n-1)x^{n-1})')
puis de remarquer que
x^{n-1}=\sum n(n-1)x^{n-1}-\sum x^{n-1}=(\sum (n-1)x^n)'-\sum x^{n-1})
et que
x^n=x^2\sum (n-1)x^{n-2}=x^2(\sum x^{n-1})')
Enfin, l'égalité
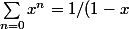)
quelques calculs de dérivées et la détermination précise des indices de début de ces sommes (impossible ici au vu de l'énoncé) permet de calculer la fonction pour tout x. A la fin on remplace x par 1/3
Bons calculs
-
Frandom94
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Mar 2020, 18:48
-
 par Frandom94 » 05 Mai 2021, 11:46
par Frandom94 » 05 Mai 2021, 11:46
Merci beaucoup !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités