En utilisant le fonction définie par
calculer les sommes suivantes : 1)
2)
Calcul de somme
4 messages
- Page 1 sur 1
Calcul de somme
par davelin » 07 Nov 2020, 17:48
Bonjour, j'aimerais un peu d'aide pour résoudre cet exercice. Merci de m'aider
En utilisant le fonction définie par = (1+x)^2^n + (1-x)^2^n)
calculer les sommes suivantes : 1)
2)
En utilisant le fonction définie par
calculer les sommes suivantes : 1)
2)
Re: Calcul de somme
par davelin » 07 Nov 2020, 18:10
Voici ce que j'ai fait pour le moment
^2^n + (1-x)^2^n = \sum_{k=0}^{2n}{(x)^k \binom {2n}{k} + \sum_{k=0}^{2n}{(-x)^k\binom {2n}{k}} })
^2^n + (1-x)^2^n = \sum_{k=0}^{2n}{(x)^k \binom {2n}{k} + \sum_{k=0}^{2n}{(-1)^k(x)^k\binom {2n}{k}} })
en dérivant par rapport à x on obtiens :
 = \sum_{k=0}^{2n}k{x^{k-1} \binom {2n}{k} + \sum_{k=0}^{2n}{(-1)^kk(x)^k^-^1\binom {2n}{k}} })
 = \sum_{k=0}^{2n}{k\binom {2n}{k}x^k^-^1(1+(-1)^k)})
a partir de la je ne vois pas comment continuer
en dérivant par rapport à x on obtiens :
a partir de la je ne vois pas comment continuer
Re: Calcul de somme
par hdci » 07 Nov 2020, 20:28
Le calcul pour f et sa dérivée me semble correct. Vous pouvez encore simplifier en séparant en 
pairs et impairs
Vous êtes sûr que dans le coefficient binomial pour
, c'est , et pas 
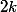
? (Car alors à un coefficient multiplicateur près, cette somme ressemble beaucoup à 
))
Vous êtes sûr que dans le coefficient binomial pour
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :