Calcul du noyau d'une matrice.

[novicemaths]

Bonsoir

Je souhaite calculer le noyau de la matrice A ci-dessous.



Voici mes calculs











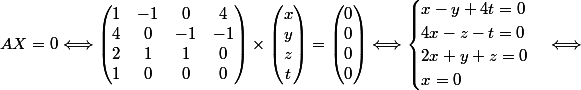
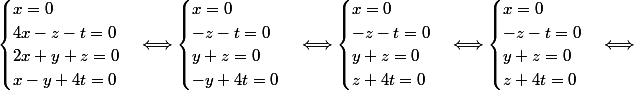
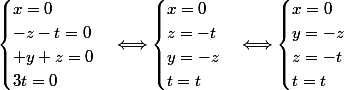
Si, bien compris le noyau de A est null.

Est-ce que mon résultat est correct ?

A bientôt

[phyelec]

Bonjour,

il y a de l'idée quand vous écrivez "Si, bien compris le noyau de A est null." Mais vous n'avez rien démontrez car
vous vous êtes trompés dans votre calcul à la dernière ligne :

x=0 oui
-z-t=0 <=> z=-t oui

y+z=0 <=> y=-z oui

3t=0 <=> t=t non

[novicemaths]

Re bonsoir

J'aurais du laisser 3t=0 ?

A bientôt

[phyelec]

non, il faut trouver t donc :
si 3t=0 que vaut t?

[novicemaths]

t=0, ce qui est plus logique.

A bientôt

[phyelec]

oui, c'est cela.

[novicemaths]

Donc au final sur ma feuille, je dois noter.

x=0
y=0
z=0
t=0

Ker(E)=0

A bientôt

[phyelec]

En faite je ne sais pas si vous avez recopié correctement votre énoncé, d'habitude on demande de calculer le noyau d'une application linéaire f représentée par une matrice (ici A)
vous avez :
X ker(f) si AX=0.
AX=0 <=> X=

A est la matrice d'une application linéaire f. Donc Kerf(f)={0 } , les "{" sont là car Ker(f) est un ensemble qui ici contient un 'élément , le vecteur null.

vous écrivez Ker(E)=0 ? pourquoi E .

si A est la matrice d'une application linéaire f :E-->F écrivez Kerf(f)={0 }

[novicemaths]

Mon énoncé demande de déterminer le noyau de la matrice.

A bientôt

[phyelec]

alors écrivez :

ker(A)={ }={0}