Calcul de double somme

par **bsangoku** » 10 Jan 2012, 20:26

Bonjour,

Je suis assez perturbé par une double somme (que je rencontre souvent ces derniers temps) et je voulais savoir comment bien le mener?

Merci d'avance

par **bsangoku** » 10 Jan 2012, 20:40

Svp aidez moi!!!

par **Le_chat** » 10 Jan 2012, 20:42

Salut. Soit tu calcules la somme des x^m, m=k+1..p puis tu refais la somme (c'est une suite géométrique)

Soit tu remarques que ta somme fait la somme de m=1 à p de la somme de k=0 à m de x^(k+m).

Il suffit de faire un dessin pour que tu voies que l'ensemble des {(m,k) où0;)k;)p et p;)m;)k+1} c'est {(m,k) où 1;)m;)p et 0;)k;)p} (en fait tu parcours ton ensemble en regardant soit la composante "k" d'abord", soit la composante "p" d'abord).

Bien sur, ça ne simplifie qu'un peu le calcul de la somme, c'est juste que les calculs seront plus faciles à gérer.

par **bsangoku** » 10 Jan 2012, 21:32

Ok et lorsqu'on tend à présent p-> +oo?

par **bsangoku** » 10 Jan 2012, 21:38

please help me!!!

par **Le_chat** » 10 Jan 2012, 22:14

Ben tu calcules ta somme pour p fixé, et tu fais p-> l'infini...

par **Dinozzo13** » 11 Jan 2012, 15:47

bsangoku a écrit:Bonjour,

Je suis assez perturbé par une double somme (que je rencontre souvent ces derniers temps) et je voulais savoir comment bien le mener?

Merci d'avance

Salut !

car il s'agit d'une somme de

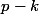
termes consécutifs d'une suite géométrique de premier terme

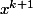
et de raison

.

Donc :

.
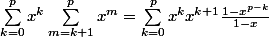Je te laisse continuer.
De toute façon, il ne s'agit que de sommes de termes de suites géométriques donc ...

:+++:

Calcul de double somme

Calcul de double somme

Qui est en ligne