Bijection dans N
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 15:27
par lomdefer » 07 Oct 2006, 15:27
Qu'est-ce qu'une bijection de

dans lui même ?
Car il faut que je détermine toute les bijection de

dans lui même telles que
 \le n)
pour tout

-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 15:29
par tize » 07 Oct 2006, 15:29
ba c'est une application injective et surjective, comme d'habitude...c'est un exercice assez classique...
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 15:45
par lomdefer » 07 Oct 2006, 15:45
classique c'est vite dit...
Pour toi sa parait basique mais pour moi ba c chaud !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 15:47
par tize » 07 Oct 2006, 15:47
Attention, je n'ai pas dit que c'était simple (pour moi) seulement que c'est un exercice classique dans le sens où je l'ai dejà vu plusieurs fois sur le net...
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 15:59
par lomdefer » 07 Oct 2006, 15:59
Et je pourrais savoir ou tu la vu car moi je ne le trouve pas et j'aimerais bien pouvoir le faire.
A moins d'une explication.... :mad:
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 16:00
par tize » 07 Oct 2006, 16:00
Une petite aide, montre que
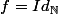
Commence comme cela : quelle peut être la valeur de f(0) ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 16:05
par tize » 07 Oct 2006, 16:05
Après avoir trouvé la valeur de f(0) recommence, quelle peut être maintenant la valeur de f(1) ? ect..
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 16:05
par lomdefer » 07 Oct 2006, 16:05
OK je vais voir sa.
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 16:17
par lomdefer » 07 Oct 2006, 16:17
Mais pour montrer que
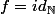
il faut utiliser les fonctions composé non ?
Mais la ou est-ce qu'il y a une deuxième fonction ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 16:20
par tize » 07 Oct 2006, 16:20
Non il ne faut pas utiliser les fonctions composées...qu'as-tu trouvé pour f(0) ?
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 16:23
par lomdefer » 07 Oct 2006, 16:23
Tu me demande quoi exactement ?
Quelle valeur j'ai trouver pour f(o) ?
Mais je ne peux trouver aucune valeur je sais juste que
 \le n)
c'est tout.
Donc je sais juste que pour

 \le 0)
.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 16:25
par tize » 07 Oct 2006, 16:25
oui et
\in\mathbb{N})
... tu connais beaucoup d'entier
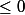
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 16:32
par lomdefer » 07 Oct 2006, 16:32
Ben la tu viens de montrer que pour tout

-
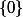
 \le n)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 16:36
par tize » 07 Oct 2006, 16:36
OK...je résume, tu as :
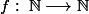
bijective et en plus
\leq n)
pour tout entier naturel

.
Donc
\in \mathbb{N})
donc f(0)=0
Ensuite
\leq 1)
combien y a-t-il d'entier naturel inférieur à 1, lesquels sont possibles etant le carctère bijectif de f
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 16:38
par lomdefer » 07 Oct 2006, 16:38
donc
=0)
donc
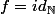
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 16:39
par tize » 07 Oct 2006, 16:39
Ensuite
\leq 1)
combien y a-t-il d'entier naturel inférieur à 1 ?, lesquels sont possibles etant le carctère bijectif de f ?
Je te suggère ensuite une recurrence
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 16:49
par lomdefer » 07 Oct 2006, 16:49
Etant donner le carctère bijectif de f, il existe qu'un seul entier naturel
)
c'est-à-dire l'entier naturel 0.
D'après l'énoncé on a
 \le n)
or etant donner le caractère bijectif de

, il éxiste qu'un seul entier naturel
)
c'est-à-dire 0.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 16:50
par tize » 07 Oct 2006, 16:50
Je pense que tu confonds

et
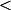
\leq 1)
donc f(1)=0 ou f(1)=1
-
lomdefer
- Membre Relatif
- Messages: 123
- Enregistré le: 17 Fév 2006, 19:06
-
 par lomdefer » 07 Oct 2006, 16:53
par lomdefer » 07 Oct 2006, 16:53
Pardon je modifie :
Etant donner le carctère bijectif de f, il existe qu'un seul entier naturel
)
c'est-à-dire l'entier naturel 0.
D'après l'énoncé on a
 \le n)
or etant donner le caractère bijectif de

, il éxiste qu'un seul entier naturel <
)
c'est-à-dire 0.
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 07 Oct 2006, 16:55
par tize » 07 Oct 2006, 16:55
Tu as lu mon dernier post, je l'ai modifié...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
 dans lui même ?
dans lui même ? dans lui même telles que
dans lui même telles que  \le n) pour tout
pour tout 
