Besoin d'aide exercice continuité

[lawick]

Bonjour à tous, j'ai actuellement un exercice à faire et je suis bloqué voici l'énoncé :
Soit f et g deux fonctions continues sur I=[0,1] telles que f rond g = g rond f.
On souhaite montrer qu'il existe l ∈ [0,1] tel que f(l)=g(l).

1) A quelle condition (satisfaite pour le reste de l'exercice) les fonction f o g et g o f sont-elles bien définies ?
2) Montrer que f admet un point fixe, càd qu'il existe a ∈ I tel que f(a)=a.

Je bloque sur ces deux questions, pour la première je pensais qu'il suffisait de dire que si f et g sont continues sur I alors g o f et f o g le sont aussi mais j'ai un énorme doute, et pour la deuxième je pensais utiliser le TVI en posant une fonction φ: I→R telle que φ(x)=f(x)-x mais pareil je ne sais pas comment me dépatouiller.
Merci d'avance pour votre aide !

[hdci]

Bonjour,

Pour la première question : on a et

Si par exemple , est-ce que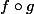 a un sens ?

Déduisez-en les deux conditions (sur f et sur g) pour que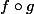 et 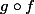aient toutes deux un sens.

Pour la seconde question : vous avez raison, il faut utiliser ; que peut-on alors dire de et de ) ? Utilisez ceci et le TVI pour montrer que 0 a bien un antécédent.

[lawick]

Merci pour votre réponse ! Pour la première question il faut donc que l'ensemble d'arrivé de f et de g soit aussi [0,1] ? Pour la seconde question si on prend x=0, φ(0)=f(0) et donc φ(0)⩾0 de même pour x=1: φ(1)=f(1)-1⩽1 et on peut ainsi utiliser le théorème des valeurs intermédiaires pour montrer que φ(x)=0 admet une unique solution sur I et par conséquent f admet un point fixe sur I c'est bien cela ?

[hdci]

Oui, c'est bien cela... Sauf

φ(1)=f(1)-1⩽1

Ce n'est pas 1 à droite...

[lawick]

Oups oui pardon c'est plutôt 0 à droite non ?

[hdci]

Oui, et maintenant effectivement vous pouvez utiliser le TVI

[lawick]

Merci pour votre aide, je rencontre un nouveau problème avec la suite de l'exercice:
On résonne par l'absurde et on suppose qu'il n'existe pas de réel l∈I tel que f(l)=g(l). On note h=f-g, et a un point fixe de f déterminé en 2)
3. Montrer que l'application h est de signe constant.
Encore merci d'avance !

[hdci]

On fait à nouveau un absurde dans l'absurde. On suppose (par l'absurde) que f(l) et toujours différent de g(l). Ce qui revient à dire que h(l) ne s'annule jamais.

Donc par l'absurde au second niveau, supposons que h ne soit pas de signe constant, sachant qu'elle est continue que peut-on en déduire ? (à nouveau ce cher TVI...)

[lawick]

Merci encore une fois pour votre réponse, donc comme on a supposé par l'absurde que h ne s'annulait jamais, on suppose (encore par l'absurde) que h n'est pas de signe constant sa continuité implique qu'elle doive s'annuler pour changé de signe absurde car on a supposé que h ne s'annulait pas c'est bien cela ?

[hdci]

Oui exactement