Arithmetique Polynome
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 17 Aoû 2007, 15:34
par Babe » 17 Aoû 2007, 15:34
Bonjour,
voila j'ai un petit souci avec cet exercice d'arithmetique




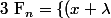(x+\mu) | \lambda,\mu\in \frac{\mathbb{Z}}{n\mathbb{Z}}\})
1) Donnez le cardinal de

2) Montrez que
}{2})
est un majorant du cardinal de

3)En deduire un minorant du nombre de polynome irreductible
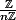
4) Que peut on dire quand n premier
5) Donnez tous les polynomes irrecductibles de

et verifiez le resultat precedent
je patoge dans le potage
merci d'avance
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 17 Aoû 2007, 16:27
par alben » 17 Aoû 2007, 16:27
Bonjour,
Il faut d'abord que tu répondes à la question 0 : Quel est le cardinal de Z/nZ.
Ensuite ça devrait aller
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 17 Aoû 2007, 16:47
par Babe » 17 Aoû 2007, 16:47
edit: j'avais ecris une horreur
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 17 Aoû 2007, 16:50
par Babe » 17 Aoû 2007, 16:50
je dirait que le cardinal de Z/nZ est egal à n ?
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 17 Aoû 2007, 16:54
par alben » 17 Aoû 2007, 16:54
La deuxième partie de ta phrase est exacte, pas la première.
Z/nZ, c'estun ensemble des classes d'équivalence. On peut l'assimiler à celui des restes dans la division euclidienne par n. Par exemple, lorsqu'on divise par 4, le reste peut être 0 ou 1 ou 2 ou 3.
edit : j'avais pas vu ton dernier message.
OK maintenant combien de
couples (a,b) et de
paires )
?
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 17 Aoû 2007, 16:58
par Babe » 17 Aoû 2007, 16:58
alben a écrit:La deuxième partie de ta phrase est exacte, pas la première.
pas compris c'est a dire ?
Z/nZ, c'estun ensemble des classes d'équivalence. On peut l'assimiler à celui des restes dans la division euclidienne par n. Par exemple, lorsqu'on divise par 4, le reste peut être 0 ou 1 ou 2 ou 3.
oui c'est comme cela que j'ai compté, donc le cardinal est bien n ?
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 17 Aoû 2007, 17:01
par alben » 17 Aoû 2007, 17:01
Oui les messages s'emmêlent un peu.
J'ai corrigé le dernier et insisté sur le fait que le rôle de a eet b n'est pas identique à celui de mu et lambda
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 17 Aoû 2007, 17:03
par Babe » 17 Aoû 2007, 17:03
je dirais n possibilité pour a et n pour b
donc Card

= 2n ?
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 17 Aoû 2007, 17:05
par alben » 17 Aoû 2007, 17:05
Perdu : ça se multiplie (essaie d'écrire tous les cas avec n=3)
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 17 Aoû 2007, 17:06
par Babe » 17 Aoû 2007, 17:06
alben a écrit:Perdu : ça se multiplie (essaie d'écrire tous les cas avec n=3)
oui c'est debile d'avoir ajouter
on obtiens donc
=n^2)
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 17 Aoû 2007, 17:10
par alben » 17 Aoû 2007, 17:10
OK et pour Card(Fn) ?
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 17 Aoû 2007, 17:12
par Babe » 17 Aoû 2007, 17:12
je dois distinguer les cas
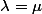
et

?
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 17 Aoû 2007, 17:20
par alben » 17 Aoû 2007, 17:20
Non c'est simplement que mu et lambda sont des racines (au signe près), donc (2,3) et (3,2) correspondent au même polynome, il ne faut pas les compter deux fois
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 17 Aoû 2007, 17:26
par Babe » 17 Aoû 2007, 17:26
j'ai essayé pour n=3 ==> card=6, pour n=4 => card=10
ca ressemble fort à la somme des k...
ca tombe bien
}{2})
enfin c'est assez intuitif la, il dois y avoir mieux comme redaction :we:
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 17 Aoû 2007, 17:42
par alben » 17 Aoû 2007, 17:42
Tu peux le faire à la main :
pour

peut prendre toutes les valeurs de 0 à n-1
pour

peut prendre toutes les valeurs de 1 à n-1
pour

peut prendre la seule valeur n
puisqu'on ne veut pas de répétitions
et là tu peux faire l'addition
Ou plus directement : il s'agit de prendre 2 valeurs parmi n+1, (la n+1 ième c'est "bis") l'ordre n'ayant pas d'importance soit

-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 17 Aoû 2007, 17:49
par Babe » 17 Aoû 2007, 17:49
pour la 3 il entende quoi par polynome irreductible ?
-
Sylar
- Membre Rationnel
- Messages: 664
- Enregistré le: 17 Juin 2007, 21:51
-
 par Sylar » 17 Aoû 2007, 18:10
par Sylar » 17 Aoû 2007, 18:10
Polynôme dont les seuls diviseurs sont les éléments inversibles ou les polynômes U.P où U est un polynôme inversible.
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 17 Aoû 2007, 18:12
par alben » 17 Aoû 2007, 18:12
Un polynome irréductible, c'est un polynome qui ne peut pas être divisé par un autre de degré au moins égal à 1.
Par exemple (X-1)(X-2) est réductible puis qu'il se divise par X-1.
Tu peux considérer que réductible, ça veut dire "factorisable", enfin si le mot existait.
Ca veut donc dire, puisque nos polynomes sont de degré 2 que irréductible est équivalent à "pas de racine".
Toutefois, pour la suite, il faut se méfier, dans Z/nZ si n n'est pas premier, un polynome du second degré peut avoir plus de deux racines.
Par exemple avec n=6, X²-X a trois racines : 0 1 et aussi 4 et X²+3X+2 en a 4 (1,2,4,5)
Edit : oui, la définition de Sylar est plus rigoureuse, pas forcément plus comprehensible
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 17 Aoû 2007, 18:26
par Babe » 17 Aoû 2007, 18:26
alben a écrit:Edit : oui, la définition de Sylar est plus rigoureuse, pas forcément plus comprehensible
oui d'accord avec toi alben
merci vais voir ce que ca donne pour la suite
-
Babe
- Membre Irrationnel
- Messages: 1186
- Enregistré le: 06 Mai 2006, 10:52
-
 par Babe » 17 Aoû 2007, 20:20
par Babe » 17 Aoû 2007, 20:20
je vois pas comment faut proceder pour la 3 :mur:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
