Arctan et intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 11 Juin 2015, 13:30
par ArtyB » 11 Juin 2015, 13:30
Bonjour,
Je cherche à calculer l'intégrale suivante:

Je peux réécrire ça:
^2} dx)
Or
=\frac{1}{1+u^2})
Donc appliqué ici avec u=x/2
 dx)
]_{2}^{n})
Est-ce correct ?

-
WillyCagnes
- Membre Transcendant
- Messages: 3754
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 11 Juin 2015, 13:36
par WillyCagnes » 11 Juin 2015, 13:36
bjr
presque bon à une facteur 2 près...
1/2[arctang(x/2)]
essaie de dériver ton résultat pour verifier

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Juin 2015, 13:37
par Ben314 » 11 Juin 2015, 13:37
Non : vu que la dérivée que tu donne pour arctan(u) est celle dans le cas où u est la variable.
Mais si u=x/2, il y a un truc en plus...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 11 Juin 2015, 13:42
par ArtyB » 11 Juin 2015, 13:42
Merci de ta réponse !
Suivant la formule suivante:
=\frac{1}{1+u^2})
J'ai:
=\frac{1}{4} * \frac{1}{1+(\frac{x}{2})^2}=\frac{1}{4} * \frac{1}{1+\frac{x^2}{4}}=\frac{1}{4+{x^2})

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Juin 2015, 13:48
par Ben314 » 11 Juin 2015, 13:48
ça c'est juste, mais... ton résultat est faux quand même du fait que la dérivée de la fonction x->arctan(x/2) n'est pas la fonction x->arctan'(x/2)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 11 Juin 2015, 13:52
par ArtyB » 11 Juin 2015, 13:52
Mais pourquoi cela ?
Je ne comprends pas, si je pose u=x/2, en appliquant la formule j'obtiens ce que j'ai écris plus haut, pourquoi en est il autrement ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Juin 2015, 13:56
par Ben314 » 11 Juin 2015, 13:56
Juste pour voir :
Vu que la dérivée de u->u² est u->2u, si "on pose" (comme tu dit) u=x/2, est ce que la dérivée de x->(x/2)² est x->2(x/2) ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 11 Juin 2015, 14:04
par ArtyB » 11 Juin 2015, 14:04
Erf oui en effet je vois... c'était stupide de ma part
Pourtant j'étais persuadé que ça allait marcher...
Merci beaucoup !
Comment faire la dérivée de arctan(x/2) dans ce cas là ? Sachant que tout ce que l'on sait c'est que arctan'(x) = 1/(1+x²) ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Juin 2015, 14:10
par Ben314 » 11 Juin 2015, 14:10
Tu n'as pas vu comment on dérive la composée de deux fonctions ?
Par exemple, tu ne sait pas dériver la fonction x->exp(2x) ?
P.S. et tu devrais nettement perdre cette très mauvaise habitude consistant à parler de "la dérivée de arctan(x/2)" : ce qu'on dérive, ce n'est pas une "formule", mais une fonction donc par exemple ici, c'est x->arctan(x/2).
Ca te permettrais en particulier de bien comprendre pourquoi x->arctan(x/2) ça ne se dérive pas de la même manière que u->arctan(u).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 11 Juin 2015, 14:27
par ArtyB » 11 Juin 2015, 14:27
Oh mon dieu faire des maths du soir au matin et du matin au soir me fait parfois vraiment perdre toute raison et tout sens commun...
Je crois que je vais aller prendre l'air là parce que quand je vois que j'en suis arrivé à poser des questions pareilles c'est qu'il est l'heure de faire une pause...
Merci beaucoup à toi, je devais vraiment avoir la tête ailleurs...
Très bonne idée concernant ton PS et la façon de formuler les choses, ça sera bien plus clair.
Un grand merci !

-
WillyCagnes
- Membre Transcendant
- Messages: 3754
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 11 Juin 2015, 16:05
par WillyCagnes » 11 Juin 2015, 16:05
ArtyB a écrit:Mais pourquoi cela ?
Je ne comprends pas, si je pose u=x/2, en appliquant la formule j'obtiens ce que j'ai écris plus haut, pourquoi en est il autrement ?
donc du=dx/2

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 11 Juin 2015, 20:41
par chombier » 11 Juin 2015, 20:41
Personnellement, pour l'intégration des fractions rationnelles, j'ai retenu cette petite formule très pratique :
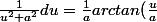 + C)
Il faut être capable de la retrouver, évidemment, mais quand on sait qu'on va avoir un examen avec ce genre de calculs, ça peut faire gagner du temps.

-
Axiom
- Membre Naturel
- Messages: 82
- Enregistré le: 22 Mai 2015, 20:10
-
 par Axiom » 11 Juin 2015, 22:10
par Axiom » 11 Juin 2015, 22:10
Bonsoir,
Il me semble Chombier que l'on peut même élargir à :
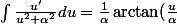 + C)
, non ? :happy:
Après, je n'ai pas refait la démonstration et je dis peut-être une grosse bêtise... :ptdr:
C'est vrai que c'est un formule vraiment très pratique et très importante que l'on retrouver dans beaucoup de primitives de fractions rationnelles, elle est vraiment à savoir..

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 11 Juin 2015, 22:33
par chombier » 11 Juin 2015, 22:33
Axiom a écrit:Bonsoir,
Il me semble Chombier que l'on peut même élargir à :
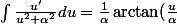 + C)
, non ? :happy:
Après, je n'ai pas refait la démonstration et je dis peut-être une grosse bêtise... :ptdr:
C'est vrai que c'est un formule vraiment très pratique et très importante que l'on retrouver dans beaucoup de primitives de fractions rationnelles, elle est vraiment à savoir..
Tout à fait mais dans ce cas je l'écrirait comme cela :
}{u^{2}(x)+\alpha^{2}}dx=\frac{1} {\alpha}\arctan(\frac{u(x)} {\alpha}) + C)
Ce qui revient à faire le changement de variable : du = u'(x) dx
Personnellement écrire u' et du dans la même formule, ça me gêne un peu. Alternative :
Une primitive de

est
)
, où u est une fonction de R dans R.
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 12 Juin 2015, 19:44
par ArtyB » 12 Juin 2015, 19:44
Merci beaucoup je l'ai notée et apprise !

-
chombier
- Membre Irrationnel
- Messages: 1324
- Enregistré le: 19 Juil 2012, 18:35
-
 par chombier » 12 Juin 2015, 19:47
par chombier » 12 Juin 2015, 19:47
ArtyB a écrit:Merci beaucoup je l'ai notée et apprise !
Est-ce que tu l'as redémontrée ? :we:
-
ArtyB
- Membre Relatif
- Messages: 460
- Enregistré le: 05 Mar 2015, 09:05
-
 par ArtyB » 12 Juin 2015, 19:55
par ArtyB » 12 Juin 2015, 19:55
Oui bien sûr !
Je déteste apprendre des choses que je ne comprends pas et en maths pour comprendre il faut démontrer :D

-
WillyCagnes
- Membre Transcendant
- Messages: 3754
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 13 Juin 2015, 10:09
par WillyCagnes » 13 Juin 2015, 10:09
bravo! tu as progressé.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
, non ? :happy: