Résoudre intégrale arctan x
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
sasie
- Membre Naturel
- Messages: 21
- Enregistré le: 16 Aoû 2009, 12:47
-
par sasie » 26 Aoû 2009, 13:37
bonjour,
voilà l'intégrale
^2} dt)
je fais un changement de variable, t=tan x
(\frac{1}{cos^{2}x})dx)
je crois qu'au niveau des bornes il n'y a pas de problemes, par contre, dans l'intégrale il y a quelque chose que je ne comprends pas car bien sur cette intégrale n'est pas possible!
merci de votre aide
-
euler21
- Membre Relatif
- Messages: 313
- Enregistré le: 26 Aoû 2009, 02:40
-
par euler21 » 26 Aoû 2009, 13:44
Bonjour
je pense que pour le changement de variables tu dois changer le nom de la variable
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
par Pythales » 26 Aoû 2009, 13:45
Pense que
-
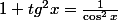
sasie
- Membre Naturel
- Messages: 21
- Enregistré le: 16 Aoû 2009, 12:47
-
par sasie » 26 Aoû 2009, 13:57
ben oui justement, je pense que ou le changement de variable n'est pas juste, ou je fais quelque chose de travers....
je devrais donc poser t= tan u, m'enfin ca ne change rien si ?
merci
-
mathelot
par mathelot » 26 Aoû 2009, 14:02
aut méthode
)
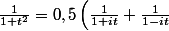au carré
^2}=0,25 \left( \frac{1}{(1+it)^2}+\frac{1}{(1-it)^2}+\frac{2}{1+t^2} \right))
à droite, se primitive en
 \right))
d'où
^2}=0,5 \left( \frac{t}{1+t^2}+arctan(t) \right))
-
sasie
- Membre Naturel
- Messages: 21
- Enregistré le: 16 Aoû 2009, 12:47
-
par sasie » 26 Aoû 2009, 17:41
merci beaucoup, bonne idée pour les complexes ! =)^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
