J'ai essayé pas mal de truc, changements de variable, tentative de réintroduction avec la formule
Merci d'avance !
Intégrale en Arctan
4 messages
- Page 1 sur 1
Intégrale en Arctan
par Aspx » 07 Nov 2007, 20:41
Bonjour, j'ai une intégrale plutôt sympathique à vous proposer.
dt)
J'ai essayé pas mal de truc, changements de variable, tentative de réintroduction avec la formule+arctan(\frac {1}{t})=\frac{\Pi}{2})
mais rien à faire...
Merci d'avance !
J'ai essayé pas mal de truc, changements de variable, tentative de réintroduction avec la formule
Merci d'avance !
par tize » 07 Nov 2007, 22:13
Bonjour,
je n'ai pas de réponse à te donner mais peut être un début avec le changement de variable=t)
on obtient :
}{1+\cos^2(x)}dx)
et ensuite avec le changement de variable : )
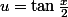j'ai :
(u^2+1)}du)
et (u^2+1)}=2\(\frac{u^2+1}{u^4+1}+\frac{-1}{u^2+1}\))
aux erreurs près :happy2: ........
c'est pas terminé mais ça me parait long il doit y avoir plus court...
je n'ai pas de réponse à te donner mais peut être un début avec le changement de variable
aux erreurs près :happy2: ........
c'est pas terminé mais ça me parait long il doit y avoir plus court...
par Aspx » 07 Nov 2007, 22:13
Je viens de trouver (si ça interesse quelqu'un).
dt = \int_{0}^{\frac {\pi}{2}} arctan(cos(u)) cos(u) du<br />\\<br />= [sin(u) arctan(cos(u))]_{0}^{\frac {\pi}{2}} + \int_{0}^{\frac {\pi}{2}} \frac {sin(u)^2}{1+cos(u)^2} du<br /><br />= \int_{0}^{\frac {\pi}{2}} \frac {1-cos(u)^2}{1+cos(u)^2} du<br />\\<br />= \int_{0}^{\frac {\pi}{2}} \frac {1-cos(u)^2+1-1}{1+cos(u)^2} du<br /><br />= \int_{0}^{\frac {\pi}{2}} \frac {2-(cos(u)^2+1)}{1+cos(u)^2} du<br />\\<br />= \int_{0}^{\frac {\pi}{2}} \frac {2}{1+cos(u)^2} - \frac {\pi}{2}<br /><br />= \int_{0}^{\frac {\pi}{2}} \frac {1}{cos(u)^2} \frac {1}{1+(\frac {1}{sqrt 2} tan(u))^2} du - \frac {\pi}{2}<br />\\<br />= [sqrt 2 arctan(\frac {1}{sqrt 2} tan(u))]_{0}^{\frac {\pi}{2}} - \frac {\pi}{2}<br /><br />= sqrt 2 \frac {\pi}{2} - \frac {\pi}{2} = (sqrt2 - 1) \frac {\pi}{2})
Pff...
Merci quand même !
Pff...
Merci quand même !
par Aspx » 07 Nov 2007, 22:15
Oups désolé j'avais pas vu ton post Tize (je postais) :marteau:
Merci pour l'aide!
A propos de la "méthode plus courte", elle m'interesse fortement! Je suis sûr qu'il y a plus astucieux (et ça m'ennerve!).
La question reste ouverte...
Merci pour l'aide!
A propos de la "méthode plus courte", elle m'interesse fortement! Je suis sûr qu'il y a plus astucieux (et ça m'ennerve!).
La question reste ouverte...
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :