Application continue

[Obito31]

bonjour,
comment montré qu'il n'existe pas d'application continue F : [0,1] --> Q(R²) ( où Q(R²) est l'ensemble des formes quadratiques sur R² ) telle que les deux conditions suivantes soient réalisées :

1) F(t) est non dégénérée pour tout t appartenant à [0,1]
2) F(0) = q0, et F(1)=q1 ( où q0 et q1 sont des formes quadratiques non dégénérées de signature différente )

[aviateur]

Bjr
C'est une conséquence directe du théorème des valeurs intermédiaires.

[Obito31]

faut montré que l'ensemble F(t) n'est pas connexe ?

[aviateur]

L'application qui a une forme quadratique associe son déterminant est continue. Donc la composée avec F est continue. Or q_0 et q_1 sont de signatures différente donc avec le th des il va exister t t.q det (F(t))=0.

[Obito31]

merci pour ta réponse !
mais je comprend pas le cas où la signature de q0 est (2,0) et celle de q1 (0,2) leur déterminant est supérieur à 0

[aviateur]

OK, j'ai pas fait attention. Je réfléchis 2 mn et je te réponds

[aviateur]

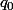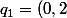Alors si les signatures sont différentes, par exemple signature (2,0) et (ça représente le cas général).
Ce n'est plus le déterminant qu'il faut regarder mais la trace qui est aussi une fonction continue.
la trace de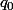 est >0 et celle de
alors il va exister t.q
si les 2 v.p de (v.p au sens de valeur propre de la matrice symétrique qui représente la forme quadratique) sont toutes les 2 nulles alors c'est terminé.

Sinon les 2 vp sont opposées, alors le déterminant est <0.
Alors on reprend mon raisonnement du post précédent mais appliqué à
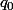et i.e sur le segment

[Obito31]

super je te remercie !

[Obito31]

par contre un truc me perturbe comment la trace de la forme reste inchangée quand on change de base alors que pour diagonalisé la matrice en utilise la transposé de la matrice de passage et non l’inverse

[aviateur]

Tu utilises la transposée si tu as normé les vecteurs propres de la matrice. Ce qui fait que P est orthogonale et
en fait

[Obito31]

j'ai pas compris je vois pas pourquoi la transposé de P est égale a l’inverse de P
parce que sa veut dire qu'on regarde q dans 2 base orthonormé .. et c'est pas sur qu'ils y on a

[aviateur]

Un exemple c'est plus parlant?


tr(Q)=tr(A)=4.
vp de A=(1,3) tr(A)=4.




tr(B)=4
Mais on a aussi


De toute façon mon raisonnement n'utilise pas vraiment le changement de base.
F(t) est de la forme avec a,b,c continues.
La trace c'est qui est continue....