Application bien définie

[marawita1]

Bonsoir,
Si on prend une application f définie d'un ensemble E dans un ensemble F.
Que signifie la question: Montrer que f est bien définie?
càd que ce qu'on doit montrer pour répondre à cette question?

[MouLou]

En général je sais pas trop ce que ca veut dire, mais par exemple la fonction racine est bien défnie sur , mais pas sur . Je saisp as trop quoi dire de plus

En gros que l'expression donnée par f(x) fait sens lorsque x est dans E

[mathelot]

cas d'école







montrer que la suite


n'est pas bien définie :we:

[mrif]

Cela veut dire que le domaine de définition de est .
Exemple: la fonction de dans est bien définie,
mais la fonction de dans n'est pas bien définie.

[mathelot]

un autre cas où la fonction n'est pas "bien définie", c'est lorsqu'elle est multivaluée
comme le logarithme complexe sur

[mrif]

un autre cas où la fonction n'est pas "bien définie", c'est lorsqu'elle est multivaluée
comme le logarithme complexe sur

.
Là on n'a plus à faire à une fonction, puisque, par définition, l'image d'un élément par une fonction est unique.

[Sylviel]

Justement, parfois on donne une fonction d'une certaine manière, et montrer qu'elle est bien définie consiste (aussi) à montrer que l'image est unique.

Exemple :
soit x la fonction qui à p associe le minimiseur de la fonction x² + px +1.
Montrer qu'elle est bien définie consiste à montrer que pour tout p la fonction x -> x²+px+1 admet un unique minimiseur :zen:

[Skullkid]

Bonjour, en général quand on demande de montrer qu'une application f de E sur F est bien définie, on demande de montrer que f satisfait bien ce qu'on attend d'une application, à savoir que chaque élément de l'ensemble de départ a exactement une image dans l'ensemble d'arrivée.

Le problème se pose souvent pour des applications qu'on définit par des formules du genre "soit f(x) le nombre qui satisfait une certaine propriété P(x)". Pour que l'application soit bien définie il faut s'assurer que pour tout x de l'ensemble de départ, il y a un et seul nombre qui satisfait P(x) dans l'ensemble d'arrivée.

Un autre cas de figure fréquent consiste à vérifier qu'une application "passe au quotient" : on part d'une application f : E -> E bien définie et on cherche à savoir si f est encore bien définie en tant qu'application de E/R dans E/R, où R est une relation d'équivalence. Par exemple, si [.] désigne la partie entière, n -> [n/2] est bien définie de Z dans Z, mais elle ne passe pas au quotient par 2Z.

[marawita1]

Merci bien à vous.
Peut être j'ai pas bien précisé ma question, en fait ici les ensembles E et F sont deux Banach et je pense que pour montrer que f est bien définie, il faudra montrer que f(x) appartient à F pour tout x dans E.
c'est ça?

[Sylviel]

Reprenons au tout début. Une application est un triplet (E,F,G) où E et F sont des ensemble et G un sous ensemble de ExF tel que, si et alors .

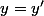Donc il faudra montrer que : pour tout x de E, f(x) est un unique élément de F.

[marawita1]

Reprenons au tout début. Une application est un triplet (E,F,G) où E et F sont des ensemble et G un sous ensemble de ExF tel que, si et alors .

Donc il faudra montrer que : pour tout x de E, f(x) est un unique élément de F.

Comment montrer que f(x) est un unique élément de F?

[Sylviel]

Tu me demandes l'équivalent de "comment résoudre une équation" ou de "comment démontrer un théorème" :zen: