Application bien définie

[mehdi-128]

Bonsoir,

Je me pose une question depuis 2 jours et j'arrive pas à comprendre le pourquoi :

Pourquoi quand on veut montrer qu'une application ou opération (exemple addition dans Z/nZ) est bien définie on veut montrer :

x=x' ===> f(x)=f(x') ?

Merci

[Viko]

C'est trés simple, il suffit d'un exemple pour comprendre. Soit f une application définit par f: x -> x^2 et un réel x par exemple 2 on a évidement 2 = 2 de plus si f(2) != f(2) (ie. 2^2 != 2^2) on a effectiment un problème, il faut donc bien x=x' => f(x) = f(x') pour que l'application f soit correctement défini

[mathelot]

on doit montrer que

pour déduire l'existence de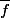 qui rend un diagramme commutatif

[Lostounet]

C'est trés simple, il suffit d'un exemple pour comprendre. Soit f une application définit par f: x -> x^2 et un réel x par exemple 2 on a évidement 2 = 2 de plus si f(2) != f(2) (ie. 2^2 != 2^2) on a effectiment un problème, il faut donc bien x=x' => f(x) = f(x') pour que l'application f soit correctement défini

Je pense que tu n'as pas compris la question de Mehdi (et c'est normal). Tu auras en fait du mal à trouver une fonction telle que x=x' et f(x)=/= f(x')...

L'application f ici est définie entre des structures algébriques.

[mathelot]

@lostounet: est ce possible de dessiner des diagrammes commutatifs sous LaTex ?

[zygomatique]

toujours des bouts de questions qui ne veulent rien dire ...

[mehdi-128]

on doit montrer que

pour déduire l'existence de qui rend un diagramme commutatif

On a pas vu les diagrammes commutatifs

[Pseuda]

Bonsoir,

On veut montrer par exemple que l'opération "somme" est bien définie dans Z/nZ. Pour cela, on dit que la "somme" de 2 classes d'équivalences est la classe d'équivalence de l'élément obtenu en faisant la somme d'un élément de 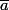et d'un élément de .

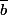Mais comme il n'y a aucune raison a priori qu'on obtienne bien toujours la même classe d'équivalence quelque soit le choix des éléments dans les classes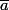 et 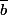, pour que cette opération soit bien définie, il faut démontrer que la classe obtenue ne dépend pas des éléments qu'on a choisis dans chaque classe et dont on fait la somme.

Le raisonnement est identique pour une fonction sur Z/nZ. Elle est bien définie si l'image d'une classe ne dépend pas de l'élément choisi dans la classe, autrement dit : .

[mehdi-128]

Bonsoir,

On veut montrer par exemple que l'opération "somme" est bien définie dans Z/nZ. Pour cela, on dit que la "somme" de 2 classes d'équivalences est la classe d'équivalence de l'élément obtenu en faisant la somme d'un élément de et d'un élément de .

Mais comme il n'y a aucune raison a priori qu'on obtienne bien toujours la même classe d'équivalence quelque soit le choix des éléments dans les classes et , pour que cette opération soit bien définie, il faut démontrer que la classe obtenue ne dépend pas des éléments qu'on a choisis dans chaque classe et dont on fait la somme.

Le raisonnement est identique pour une fonction sur Z/nZ. Elle est bien définie si l'image d'une classe ne dépend pas de l'élément choisi dans la classe, autrement dit : .

Ah je vois par exemple dans Z/3Z comme on a et on doit avoir si on note





C'est ça ?

[Pseuda]

Ah je vois par exemple dans Z/3Z comme on a et on doit avoir si on note





C'est ça ?

Oui, dans ce cas, f est la fonction somme de 2 variables (classes d'équivalences) dans Z/3Z. Et on a bien :

: la somme de 2 classes d'équivalence ne dépend pas des représentants choisis dans chaque classe, donc elle est bien définie.