Anneau et nilpotence

par **Ncdk** » 04 Oct 2015, 10:31

Bonjour,

J'avais une question sur un exercice, mais j'avoue que j'ai pas compris la résolution :ptdr:

Soit A un anneau et N(A) l'ensemble de ses éléments nilpotents.

Dans l'exercice on a montré que :
1) N(A) est un idéal de A
2) Soit I un idéal de A,

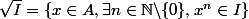
est un idéal de A contenant I et N(A)

Je dois déterminer

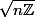
et

par **zygomatique** » 04 Oct 2015, 10:45

salut

tout d'abord déterminer N(Z/nZ) ...

quels sont les éléments nilpotents de Z/nZ ?

par **Ncdk** » 04 Oct 2015, 10:55

Je sais pas si ça répond correctement mais on a vu que par exemple :

,

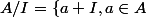
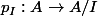
qui est la projection canonique, et cette application est surjective.
Donc

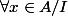
s'écrit

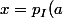où

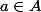
Donc pour savoir qui est

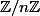
c'est

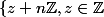
et faut trouver les éléments nilpotents de cette ensemble si je dis pas de bêtises.

par **zygomatique** » 04 Oct 2015, 11:46

a ben si tu ne sais pas déjà ce qu'est Z/nZ (ensemble des restes modulo n) ....

(Z/nZ, +, *) est un anneau

nilpotent ? pour l'addition ou la multiplication ?

par **Ncdk** » 04 Oct 2015, 12:10

Je connais, du moins je connais mais avec une belle partie de flou, pour ça que je sais pas ce que je fais.

En gros si on prend l'élément n de Z/nZ, on peut le décomposer en produit de facteurs premiers

Donc on peut écrire

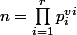
. Mais la question que je me pose déjà c'est de savoir si je prends un élément

si je lélève à la puissance

alors il vaudra 0 ou pas ? Si oui, x est un élément nilpotent de Z/nZ.

Du coup c'est nilpotent pour la multiplication pour répondre à ta question

par **MouLou** » 04 Oct 2015, 12:17

Ncdk a écrit:Je connais, du moins je connais mais avec une belle partie de flou, pour ça que je sais pas ce que je fais.

En gros si on prend l'élément n de Z/nZ, on peut le décomposer en produit de facteurs premiers

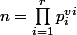
Donc on peut écrire . Mais la question que je me pose déjà c'est de savoir si je prends un élément si je lélève à la puissance alors il vaudra 0 ou pas ? Si oui, x est un élément nilpotent de Z/nZ.

Du coup c'est nilpotent pour la multiplication pour répondre à ta question

Avec cette approche tu te rapproche de la réponse, mais c'est pas cela. La question peut effectivement etre reformulée de la manière suivante: quels entiers compris entre 0 et n-1 sont tels qu'élevés à une certaine puissance ils deviennent un multiple de n. Si tu regardes la décomposition de n en facteurs premiers (et en utilisant lemme de gauss etc sur les nombres premiers), à quelles conditions

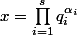
est un tel nombre?

par **zygomatique** » 04 Oct 2015, 12:20

oui c'est ça

ex : n = 12 alors 6^2 = 36 = 3 * 12 = 0 dans Z/12Z donc 6 est nilpotent ....

tu dois maintenant pouvoir donner tous les éléments nilpotents de Z/nZ dans le cas général ....

par **Ncdk** » 04 Oct 2015, 12:47

Je vois pas, j'ai une idée quand même !

C'est quand les

divise x non ?

par **zygomatique** » 04 Oct 2015, 13:07

regarde mon exemple ...

6 est nilpotent ...

2 est-il nilpotent ?
3 est-il nilpotent ?

par **Ncdk** » 04 Oct 2015, 13:14

Non 2 et 3 ne sont pas nilpotents. Par contre

est nilpotent qui est 6.

Donc si on généralise c'est surement le

est nilpotent non ?

EDIT : Je crois que j'ai parlé trop vite.

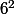
c'est

donc

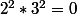
Donc 2 et 3 sont nilpotents au final. Et comme ils sont nilpotents, leur PPCM aussi.

par **zygomatique** » 04 Oct 2015, 14:55

ben non !!!

existe-t-il n tel que 2^n = 0 ?

par **Ncdk** » 04 Oct 2015, 16:36

En fait comment je peux le prouver qu'il existe pas 2 nilpotent dans ton exemple ? :doh:

par **zygomatique** » 04 Oct 2015, 17:01

aucune puissance de 2 n'est multiple de 12 ...

dans Z/12Z le seul élément nilpotent est 6 ...

dans Z/24Z les éléments nilpotents sont 6 et 12 ....

par **Ncdk** » 04 Oct 2015, 17:34

D'ailleurs pour n premiers, il n'y a pas d'éléments nilpotents non ?

par **MouLou** » 04 Oct 2015, 22:16

C'est exact. ce que veut te faire comprendre Zygomatique, c'est: quelle est la décomposition en facteur premier de 12? de 6? vois tu un point commun entre les 2? peux tu généraliser?

par **Ncdk** » 05 Oct 2015, 18:32

Oui je vois, que 12 c'est bien

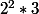
Qui est bien la décomposition en produit de facteurs premiers.

Mais le 6 je le vois seulement car c'est le PPCM de 2 et 3.
Mais je ne sais pas si c'est exact, ou s'il y a quelque chose de plus subtil à trouver.

EDIT : Pour moi j'avais pensé à dire que 2 divise 12 et 3 divise 12, donc du coup comme c'est des nombres premiers 2*3 divise 12. Propriété que j'avais oublié :mur:

par **MouLou** » 05 Oct 2015, 23:26

Je pense que tu as compris mais à te lire j'arrive pas à en être persuadé. Donc je vais te demander de me donner un nilpotent de

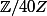
, et même tous en fait.

Edit: En fait tu dis PPCM, mais PPCM de quoi? le PPCM de quoi prendrais tu si tu avais affaire à un entier n quelquonque? Et d'une manière générale, oui c'est un poil plus subtil que le PPCM

par **Ncdk** » 06 Oct 2015, 07:38

Ce que je pensais en parlant de PPCM c'était de faire le PPCM des facteurs premiers, c'est-à-dire de chaque facteurs premiers.

Mais je sais pas si réellement on les aurait tous (les éléments nilpotents).

EDIT : Comme tu as dis j'ai pas totalement compris la chose, faudra déjà que je sache trouver les éléments nilpotents de Z/nZ ou n est un entier, avant de regarder le cas général, car je ne vois pas le fonctionnement de la chose x)

par **Robot** » 06 Oct 2015, 08:08

L'image de l'entier a dans Z/nZ est un nilpotent si et seulement si a est divisible par tous les diviseurs premiers de n, autrement dit si et seulement si a est divisible par le produit des diviseurs premiers de n.

Anneau et nilpotence

Anneau et nilpotence

Qui est en ligne