Nilpotence dans un anneau

[Lostounet]

Hello,

Considérons (A, + , x) un anneau non trivial. Je suppose a, b éléments nilpotents de A qui commutent.
Je dois d'abord montrer que a + b et ab sont nilpotents.

Je ne sais pas si c'est bon:

Il existe n,m dans N* tq:


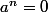
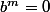
Deux cas se présentent. Soit m > n soit n n, alors il existe p>0 tel que m = n + p




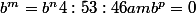
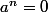
J'ai fait le produit en faisant apparaitre du vu que c'est commutatif je peux faire ça, puis j'ai exhiber un b^-p en produit pour trouver donc que (ab) nilpotent.

Est-ce que c'est bon?

[DamX]

hello,

c'est presque trop compliqué selon moi.

a et b commutent donc élever ab à une puissance k se fait classiquement (ab)^k = a^k.b^k

Il ne reste plus qu'à bien choisir k pour être sur que ça s'annule, je te laisse voir ce qui convient, c'est pas bien compliqué.

Quant à a+b, comme a e tb commutent la formule du binome s'applique et encore une fois il faudra bien choisir la puissance.

Damien

[Lostounet]

Peut-être que je peux choisir un multiple de n et de m !

k = mn

Je prends donc

Comme a^n = 0 et b^m = 0, je peux choisir k = mn

?

[DamX]

Peut-être que je peux choisir un multiple de n et de m !

k = mn

Pour ab ? Oui ça va marcher, m'enfin il y a aussi beaucoup plus petit comme puissance possible !

[Lostounet]

Je ne vois pas?

Pour le (a + b)^n nilpotent, je vais utiliser le binome de Newton:





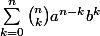
Heu je dois essayer de trouver une somme nulle. J'ai pensé à multiplier par


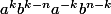
Comme ça je fais apparaitre du (ab)^n en somme, que je peux supposer nul... Un peu bourrin et bête.

[DamX]

Je ne vois pas?

Pour le (a + b)^n nilpotent, je vais utiliser le binome de Newton:





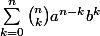
Heu je dois essayer de trouver une somme nul. J'ai pensé à multiplier par


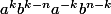
Comme ça je fais apparaitre du (ab)^n en somme, que je peux supposer nul... Un peu bourrin et bête.

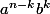
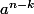
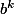
pas besoin de multiplier ou de gérer des puissances négatives. Quand tu as des termes , quelles conditions mettre sur n pour etre sur que chacun de ces termes soit nul ? sous-entendu pour que ces termes soit nul il faut ou , c'est à dire soit n-k >= p (je renote p l'indice de nilpotence de a), ou bien k >= m (indice de nilpotence de b).
Comment prendre le n pour garantir ça pour tous les k ?

------

Pour revenir au cas (ab)^k = a^kb^k, tu vois que prendre k = min(p,m) va suffire pour que soit a^k soit nul ou bien b^k soit nul, mais ton k=mp marchait aussi à fortiori

[Lostounet]

Hmm...

On veut donc ces deux conditions: n - p>= k >= m ?

[jlb]

Hmm...

On veut donc ces deux conditions: n - p>= k >= m ?

bonsoir, écris plutôt n>k+p et k>m donc n>...

[Lostounet]

n > m + p..? On cherche des conditions sur n alors

[jlb]

n > m + p..? On cherche des conditions sur n alors

c'est ça!! tu prends n=m+p , pour k tel que 0=m les puissances de a sont nulles ( ou vice versa, j'ai trop lu )

[deltab]

Je ne vois pas?

Pour le (a + b)^n nilpotent, je vais utiliser le binome de Newton:





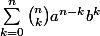
Heu je dois essayer de trouver une somme nulle. J'ai pensé à multiplier par


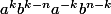
Comme ça je fais apparaitre du (ab)^n en somme, que je peux supposer nul... Un peu bourrin et bête.

Eviter et , et sont déjà réservés
Considérer plutôt (a+b)^p.
(a+b)^p=\sum_{k=0}^p {p \choose k}a^{p-k}b^k.
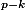
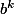
Si pour tout l'un des facteurs a ou est nul, alors , il suffit pour cela que 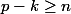et 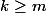ce qui donne