Analyse
5 messages
- Page 1 sur 1
Re: Analyse
Bonjour, je bloque sur cet exercice.
Pouvez-vous m'aider svp?
Soit h la fonction\longrightarrow h(x,t)=\frac{xtsin(t)}{x^2-2xcos(t)+1}) et
et
I=}{1-cos(t)}dt)
Montrer que I est convergente. Dans ce qui suit, nous présenterons deux méthodes de calcul de I.
Montrer que l'application H:=\int_{0}^{\pi} \frac{xtsin(t)}{x^2-2xcos(t)+1}dt) est continue sur [0,1].
est continue sur [0,1].
Determiner les suites) vérifiant la relation de recurrence suivante:
vérifiant la relation de recurrence suivante:
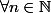 ,
, s_{n+1}+s_{n}=0) pour
pour 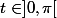
Montrer que pour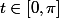 l'application
l'application ) est développable en série entière au voisinage de 0.
est développable en série entière au voisinage de 0.
Soit alorsx^n) ce développement en serie entière et R son rayon de convergence.
ce développement en serie entière et R son rayon de convergence.
Déterminer l'expression des coefficients) . Que peut-on dire de R?
. Que peut-on dire de R?
Soit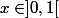 fixé.
fixé.
Montrer que la série) converge normalement sur
converge normalement sur 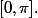
En deduire que H est développable en serie entière au voisinage de 0.
Exprimer H(x) a l'aide de fonctions élémentaires pour tout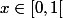 .
.
En déduire la valeur de I.
On considère l'équation différentielle:
(E):+y(x)=\frac{1}{x\sqrt{1-x^2}}-\frac{1}{x(1+x)})
Résoudre (E) sur ]0,1[
Existe-t-il une solution de (E) se prolongeant par continuité sur [0,1] ?
Soit=\frac{1}{\pi} \int_{0}^{\pi}\frac{tsint(t)}{1-xcos(t)}dt)
Montrer que est une application continue sur [0,1], dérivable sur ]0,1[.
est une application continue sur [0,1], dérivable sur ]0,1[.
Monter que est une solution de (E) sur ]0,1[.
est une solution de (E) sur ]0,1[.
Retrouver la valeur de I.
La première question ne pose pas de problème, j'aurais juste besoin de pistes pour les autres.
Pouvez-vous m'aider svp?
Soit h la fonction
I=
Montrer que I est convergente. Dans ce qui suit, nous présenterons deux méthodes de calcul de I.
Montrer que l'application H:
Determiner les suites
Montrer que pour
Soit alors
Déterminer l'expression des coefficients
Soit
Montrer que la série
En deduire que H est développable en serie entière au voisinage de 0.
Exprimer H(x) a l'aide de fonctions élémentaires pour tout
En déduire la valeur de I.
On considère l'équation différentielle:
(E):
Résoudre (E) sur ]0,1[
Existe-t-il une solution de (E) se prolongeant par continuité sur [0,1] ?
Soit
Montrer que
Monter que
Retrouver la valeur de I.
La première question ne pose pas de problème, j'aurais juste besoin de pistes pour les autres.
Re: Analyse
Bionjour,
Aucune trace du mondre effort de recherche. Le seul effort est de poster l'énoncé sur tous les forums mathématiques disponibles, en espérant que quelqu'un voudra bien faire le travail à la place du posteur.
Ce n'est pas une démarche à encourager !
Aucune trace du mondre effort de recherche. Le seul effort est de poster l'énoncé sur tous les forums mathématiques disponibles, en espérant que quelqu'un voudra bien faire le travail à la place du posteur.
Ce n'est pas une démarche à encourager !
Re: Analyse
Bonjour, pour votre remarque.
J'ai avancé sur le sujet et si j'ai pris la peine de recopier ce sujet, c'est que j'étais coincé.
Si vous pouvez apporter de l'aide juste pour le développement en série, j'apprécierai.
Je tiens à préciser qu'en appliquant les méthodes, les coefficients sont atroces et ne donnent pas envie.
Merci
J'ai avancé sur le sujet et si j'ai pris la peine de recopier ce sujet, c'est que j'étais coincé.
Si vous pouvez apporter de l'aide juste pour le développement en série, j'apprécierai.
Je tiens à préciser qu'en appliquant les méthodes, les coefficients sont atroces et ne donnent pas envie.
Merci
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
