Analyse

par **deltab** » 02 Aoû 2014, 15:55

marcopolo20 a écrit:u'(g'ou)

en fait je ne connais pas encore l'allure de la courbe puisque je n'arrive pas à étudier f'

Pour

,

et

Ne me dis pas maintenant que tu ne sais pas étudier le signe de

.

par **marcopolo20** » 02 Aoû 2014, 16:06

deltab a écrit:Pour , et
Ne me dis pas maintenant que tu ne sais pas étudier le signe de .

mais la fonction est f(x)=(racine de x) *ln(x²)

par **marcopolo20** » 02 Aoû 2014, 16:12

deltab a écrit:Pour , et
Ne me dis pas maintenant que tu ne sais pas étudier le signe de .

ok merci beaucoup mais je ne vois pas comment vous avez fait pour mettre au même dénominateur

par **zygomatique** » 02 Aoû 2014, 16:37

marcopolo20 a écrit:ok merci beaucoup mais je ne vois pas comment vous avez fait pour mettre au même dénominateur

il suffit de savoir que tout nombre positif est le carré de sa racine carrée ...

:ptdr:

par **marcopolo20** » 02 Aoû 2014, 16:52

zygomatique a écrit:il suffit de savoir que tout nombre positif est le carré de sa racine carrée ...

:ptdr:

Ah oui c bon merci

par **marcopolo20** » 03 Aoû 2014, 20:47

Bonsoir,

J'ai encore des problème avec cette fonction, cela concerne l'étude des variations.

Pour x>0, f'(x)=(ln(x)+2)/

qui s'annule en e^-2
Pour cette dérivée dans le tableau de dérivée la méthode signe contraire de a, signe de a ne fonctionne pas et je ne comprend pas pourquoi.
Pourx<0, f'(x)=(4-ln(x²))/2

qui s'annule en -e^2

De plus la fonction est paire donc les dérivées devraient s'annulées en a et en -a non ?

merci de votre aide

par **deltab** » 03 Aoû 2014, 21:08

Bonsoir

Pour x>0, f'(x)=ln(x)+2/

On dirait que tu le fais exprès

par **marcopolo20** » 03 Aoû 2014, 21:27

deltab a écrit:Bonsoir

On dirait que tu le fais exprès

pardon, le - était en trop

par **deltab** » 03 Aoû 2014, 22:04

marcopolo20 a écrit:pardon, le - était en trop

et le

aussi, x>0

par **deltab** » 03 Aoû 2014, 23:01

Pour cette dérivée dans le tableau de dérivée la méthode signe contraire de a, signe de a ne fonctionne pas

Tu fais apparemment référence au signe de

,

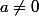
. Je ne vois pas cette expression dans la dérivée. Étudies

pour

, (

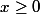
est paire).

par **marcopolo20** » 04 Aoû 2014, 09:28

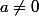
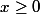
deltab a écrit:Tu fais apparemment référence au signe de , . Je ne vois pas cette expression dans la dérivée. Étudies pour , ( est paire).

Non, je ne fais pas référence a une équation du second degré car là, c'est : une équation du second degré est du signe de a sauf entre les racines lorsqu'elles existent mais pour une équation du type ax+b=0, c'est : signe contraire de a, puis 0, signe de a mais je suppose que c'est à cause du ln que cela ne fonctionne pas non ?
Pour l'autre question, j'ai compris merci.

par **deltab** » 05 Aoû 2014, 22:16

Bonsoir

marcopolo20 a écrit:Non, je ne fais pas référence a une équation du second degré car là, c'est : une équation du second degré est du signe de a sauf entre les racines lorsqu'elles existent mais pour une équation du type ax+b=0, c'est : signe contraire de a, puis 0, signe de a mais je suppose que c'est à cause du ln que cela ne fonctionne pas non ?
Pour l'autre question, j'ai compris merci.

Tu avais à résoudre l'équation pour

:

. Pourquoi veux-tu utiliser les propriétés de l'équation

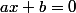
à l'équation

pour laquelle il faut utiliser les propriétés de la fonction

Analyse

Qui est en ligne