Analyse

[marcopolo20]

Merci de votre aide

[Joker62]

Hello,

Le nombre de Joker tiré suit une loi Binomiale.
Il faut juste trouver l'expérience de Bernoulli associée, combien de fois on la répète et quelle est la probabilité du succès de cette épreuve.

[marcopolo20]

J'ai un autre problème avec un autre exo :

f(x)= (racine de x)ln(x²) si x>0
0 si x=0
(racine de -x)ln(x²) si x<0

Il faut étudier la parité de la fonction, faut 'il étudier la parité pour chaque intervalle ? Et f(-x) est impossible pour x>0 et x<0, faut 'il en conclure que la fonction est impaire sur ces intervalles ? Et pour x=0 je ne vois pas.

Merci de votre aide.

[MacManus]

[quote="marcopolo20"]J'ai un autre problème avec un autre exo :

f(x)= (racine de x)ln(x²) si x>0
0 si x=0
(racine de -x)ln(x²) si x0 et x0 et tout x<0)
f(x) = 0 pour x=0

[marcopolo20]

En fait tu peux réécrire ta fonction f comme étant définie par
f(x) = pour tout x réel non nul (pour tout x>0 et tout x<0)
f(x) = 0 pour x=0

oui mais je ne vois pas comment étudier la parité avec cette écriture

[MacManus]

Et bien |-x| = ? et (-x)² = ?
et f(-0)=f(0)=0

ps: ça aurait été quand mieux pour celles ou ceux qui raffolent des probas, de créer un nouveau topic sur ton pb d'analyse...

[marcopolo20]

Et bien |-x| = ? et (-x)² = ?
et f(-0)=f(0)=0

ps: ça aurait été quand mieux pour celles ou ceux qui raffolent des probas, de créer un nouveau topic sur ton pb d'analyse...

|-x|= x si x0

(-x)² = x

[MacManus]

|-x|= -x si -x>0 càd si x<0
|-x|= -(-x) si -x<0 càd |-x| = x si x>0

Donc |-x| = |x|

tu peux voir aussi que |-x| = |(-1)x| = |-1| |x| = |x|

(-x)² = x²

[marcopolo20]

|-x|= -x si -x>0 càd si x0

Donc |-x| = |x|

tu peux voir aussi que |-x| = |(-1)x| = |-1| |x| = |x|

donc f(-x) = f(x) et f est paire ?

[Ingrid55]

Tu dois vérifier si la soustraction des deux égalités donne 0 c-a-d f(-x) - f(x) = 0 , donc f est paire .
Pour f impaire , on a l'égalité f(-x) = - f(x) .

[MacManus]

donc f(-x) = f(x) et f est paire ?

f est paire oui

[marcopolo20]

Ensuite, il faut étudier les variations de f et je trouve qu'elle est croissante sur ]-infini,0[ alors que le calculatrice me dit l'inverse. Est-ce que le dérivé de racine de -x est 1 / 2 racine de -x ?

[zygomatique]

non .................................

[deltab]

Bonsoir.

non .................................

et encore NON .................................
@ marcopolo20
Est-il nécessaire d'étudier une fonction paire sur
Si et dérivable en un point , alors

[marcopolo20]

En étudiant la dérivabilité en 0, je tombe sur une forme indéterminée 0/0 et je ne vois pas comment déterminer le limite en 0 de racine(|x|)ln(x²)/x


Merci de votre aide

[marcopolo20]

Bonsoir.

et encore NON .................................
@ marcopolo20
Est-il nécessaire d'étudier une fonction paire sur
Si et dérivable en un point , alors

mais en montrant que f est croissante sur ]0,+infini[ on peut en déduire que f est décroissante sur ]-infini,0[ puisque la fonction est paire et que donc sa courbe est symétrique par rapport à l'axe des ordonnées non ? Car le je ne vois pas ce que vous voulez dire.

J'ai trouver pour x>0, f'(x)=ln(x²)+2racine(2racinex)/2racinex et je ne vois pas comment étudier le signe du numérateur ?

Merci de votre aide

[deltab]

Bonjour

mais en montrant que f est croissante sur ]0,+infini[ on peut en déduire que f est décroissante sur ]-infini,0[ puisque la fonction est paire et que donc sa courbe est symétrique par rapport à l'axe des ordonnées non ? Car le je ne vois pas ce que vous voulez dire.

J'ai trouver pour x>0, f'(x)=ln(x²)+2racine(2racinex)/2racinex et je ne vois pas comment étudier le signe du numérateur ?

Merci de votre aide

Le NON de zygomatique et de moi a lieu pour la dérivée de .

Comment as-tu trouvé que f est croissante sur

[marcopolo20]

Bonjour



Le NON de zygomatique et de moi a lieu pour la dérivée de .

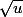
mais je ne comprend pas pourquoi car ()'=1/(2())
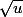
d'après la formule non ?

[deltab]

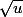
mais je ne comprend pas pourquoi car ()'=1/(2())
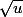
d'après la formule non ?

Il manque effectivement le facteur .
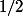
On voulait te faire remarquer le signe dans
Quelle est la dérivée d'une fonction composée?

[marcopolo20]

Quelle est la dérivée d'une fonction composée?

u'(g'ou)

en fait je ne connais pas encore l'allure de la courbe puisque je n'arrive pas à étudier f'