Analyse fonctionnelle

[marie49]

Bonjour à tous!
Je suis toujours sur mon devoir maison d'analyse fonctionnelle, dans un autre exercice cette fois c'est pourquoi j'ouvre un nouveau post.
Voici le problème :

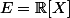
Soit normé par

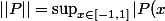Montrer que :

On a une indication :

Indication : on pourra considérer l'application linéaire

J'ai étudié la continuité de l'application u et j'ai montré que u était discontinue en tout point de E.
Après j'ai écrit des trucs mais je pense que je suis sur la mauvaise piste...

u est discontinue en tout point signifie bien que : ?

Mais après je vois pas comment trouver Q tel que Q(2)=0.

Merci d'avance à ceux (ou celles!) qui pourront m'aider!

[alavacommejetepousse]

bonsoir

connais tu ce résultat pour une forme linéaire non nulle u sur un evn E

H = ker u


u continue ssi H est fermé

et lorsque H non fermé H est dense dans E

[marie49]

J'ai vérifié dans mon cours à tout hasard, mais nous n'avons pas vu ce résultat...
Donc je pense pas pouvoir l'utiliser.

Il n'y a pas d'autre manière de repondre a la question?

[alavacommejetepousse]

sisi bien sûr mais ça va revenir en gros à ça je pense

[marie49]

ok, ben je vais y réfléchir alors!
merci

[alavacommejetepousse]

si P(2) = 0 rien à faire
si non
on peut supposer P(2) = 1 quitte à diviser P par P(2)
u est discontinue au point P

il existe une suite Pn de limite P avec u(Pn) qui ne tend pas vers P(2)

posons H = ker u

H et vect (P) sont supplémentaires
on peut écrire

Pn = Hn + a(n) P avec Hn dans H et a(n) dans R

u(Pn) = a(n) ne tend pas vers 1 il existe un réel r>0 et une sous suite
a(phi(n) avec la(phi(n) - 1 l >r

par commodité je continue à l'appeler a(n)

on a (Pn - P )/(-a(n) + 1) = Hn / (1-a(n) ) - P

ceci prouve que la suite Qn = Hn /(1-(a(n)) converge vers P tout en étant dans H

et répond à ta question

[marie49]

Merci beaucoup! Ca fait deux fois que tu m'aides en deux jours!
J'ai pas trop le temps de regarder maintenant, mais avec ca je devrais m'en sortir!
Encore merci!