Analyse convexe

[ZLM]

Bonsoir, s'il vous plaît aidez-moi à résoudre cet exercice.

Exercice

1)Les ensembles définis de la manière suivante :

a)
et


b)
et

Sont-ils proprement séparés et fortement séparés par la forme linéaire
?
Ou simplement par l'hyperplan associé ou ne le sont par l'hyperplan correspondant ?
Merci d'avance.

[ZLM]

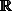
Dans tout les ensembles exposant , pas exposant Alpha.

[pascal16]

quelques précisions :
n>=2 pour que la définition ait un sens ?
x1 : est la première coordonnée du vecteur x ?

si tu as les définitions qui vont avec, je veux bien me pencher dessus

[ZLM]

Bonsoir pascal16,
vous avez raison.
et est la première cordonnée du vecteur

[pascal16]

représentation en géométrie dans l'espace classique "0,x,y,z"

cas a :
S est un demi-plan inclus dans Oyz, dans ce plan y>=50
T est un disque de rayon 1 inclus dans Oyz
ils sont tout à fait séparable par un hyperplan y=cst avec 1<y<50, mais pas par un hyperplan x=cst


cas a :
S est un demi-plan inclus dans Oyz, dans ce plan y>=50
T est la moitié de l'espace x=>1
ils sont tout à fait séparable par un hyperplan x=cst avec 0<x<1

f(x)=x1
f(x, x<0) : n'inclus ni S ni T
f(0) : inclus tout S.
f(0<x<1) : n'inclus ni S ni T
f(x, >=1) : inclus une partie de T et pas S

[ZLM]

Bonjour pascal16,
un très grand merci à vous. Merci beaucoup.