Bonjour, quelqu'un peut-il m'aider à résoudre cet exercice?
Soit

une fonction convexe sur
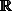
deux fois dérivable. La fonction

étant définie sur

par
=g(||x||))
, déterminer la matrice Hessienne

de

. Déterminer les valeurs propres de cette matrice pour
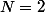
.

Poser
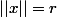
où
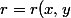)
pour
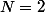
et calculer
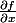
,
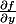
,

,

et

.
Ensuite généraliser à l'ordre

après avoir écrit la Hessienne et déterminer les valeurs propres pour
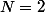
Voici ce que j'ai fait.
Pour
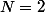
calculons les dérivées partielles.
Après dérivée j'obtiens :
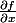
=
}{\partial x})
;
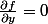
;
}{\partial x}+ \frac{\partial g}{\partial r} \times \frac{\partial^2 r(x,y)}{\partial x^2})
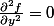
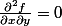
=

.
Ainsi on obtient la matrice Hessienne pour
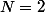
:
}{\partial x}+ \frac{\partial g}{\partial r}\times \frac{\partial^2 r(x,y)}{\partial x^2}& 0 \\ 0 & 0 \end {pmatrix}\quad)
Maitenant si mes calculs de dérivées partielles sont justes ainsi que la matrice Hessienne, mon soucis est comment généraliser cette matrice à l'ordre

