A K-algebre integre de dim finie => A corps

par **Dyo** » 30 Nov 2008, 09:52

Bonjour,

Voici une propriété qui est sûrement pas très difficile à montrer, mais je bloque :marteau:

Si

est un corps commutatif, soit

une

-algèbre (donc anneau) intègre et de dimension (en tant qu'ev) finie.
Alors comment en déduire que

est un corps ?

Merci pour votre aide.

par **ThSQ** » 30 Nov 2008, 10:03

Chais pas un truc style :

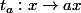
est linéaire injective donc bijective ;-)

par **Dyo** » 30 Nov 2008, 10:22

Ca c'est pour démontrer qu'un anneau intègre fini est un corps nan ?
:mur:

A est à dimension finie (pas nécessairement fini). Ou alors j'ai loupé un truc :p

par **leon1789** » 30 Nov 2008, 11:03

Dyo a écrit: Ou alors j'ai loupé un truc :p

oui, c'est quasiment pareil : ici, c'est autre chose qui est fini(e) ...

par **ThSQ** » 30 Nov 2008, 11:10

Dyo a écrit:Ca c'est pour démontrer qu'un anneau intègre fini est un corps nan ?
:mur:

A est à dimension finie (pas nécessairement fini). Ou alors j'ai loupé un truc :p

Tout pareil, l'idée est la même : comment passer de injectif à bijectif.

par **Dyo** » 30 Nov 2008, 11:28

Oula oui ... je ne pensais plus du tout qu'en dim finie, pour un opérateur, on avait injectif <=> bijectif... :cry:

*honteux* :briques:

Merci du coup, la démo devient la même, et c'est évident.

A K-algebre integre de dim finie => A corps

A K-algebre integre de dim finie => A corps

Qui est en ligne