Q n'admet pas de borne supérieur
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
StupideMoi
- Membre Naturel
- Messages: 20
- Enregistré le: 22 Déc 2012, 13:42
-
 par StupideMoi » 03 Jan 2013, 13:54
par StupideMoi » 03 Jan 2013, 13:54
Salut à tous :lol3:!!
Je suis en train de comprendre la solution de l'exercice suivant:
Montrer que l'ensemble X = { x;);) : x²<2 } n'admet pas de borne supérieur dans ;).
Voici la solution:
On a X = { x;);) : -V2 < x < V2 }
Il est clair que ;)x;)X, ;)y;)Y, on a x;)y. Montrons que c;)X et c;)Y. Supposons que c;)X, c'est à dire c...
Mes questions sont:
1. Pourquoi il faut considérer un autre ensemble Y, n'est-il pas suffisant d'utiliser un seul ensemble X?
2. Comment sommes-nous arrivés à 1/n < (2-c²)/(2c+1) (je sais que c'est avec la méthode de Héron mais comment)?
3. Pouvons-nous simplement prouver que V2;);), alors l'ensemble X n'admet pas de borne supérieur dans ;)?
S'il vous plaît aidez-moi, je ne sais pas quoi faire :triste:!!
Merci beaucoup pour votre temps :we:!!

-
eratos
- Membre Relatif
- Messages: 280
- Enregistré le: 30 Oct 2009, 13:23
-
 par eratos » 03 Jan 2013, 16:30
par eratos » 03 Jan 2013, 16:30
StupideMoi a écrit:3. Pouvons-nous simplement prouver que V2;);), alors l'ensemble X n'admet pas de borne supérieur dans

?
S'il vous plaît aidez-moi, je ne sais pas quoi faire :triste:!!
Merci beaucoup pour votre temps :we:!!
si V2 est dans Q, il existe p,q dans N et Z* tel que p/q=V2 avec p et q premier entre eux (sinon on peut réduire la fraction).
On a en élevant au carré, p²=2q². p² est pair donc p aussi(tu le prouve simplement avec la contre apposée). Donc il existe k dans Z tel que (2k)² =4k² =2q² càd 2k²=q². Donc que q est pair . Ce qui contredit que le pgcd de p et q vaut 1. Autrement dit tels p et q n'existent pas :lol3:
-
StupideMoi
- Membre Naturel
- Messages: 20
- Enregistré le: 22 Déc 2012, 13:42
-
 par StupideMoi » 03 Jan 2013, 16:47
par StupideMoi » 03 Jan 2013, 16:47
On a en élevant au carré, p²=2q². p² est pair donc p aussi(tu le prouve simplement avec la contre apposée). Donc il existe k dans Z tel que (2k)² =4k² =2q² càd 2k²=q². Donc que q est pair . Ce qui contredit que le pgcd de p et q vaut 1. Autrement dit tels p et q n'existent pas :lol3:
OK, merci beaucoup pour votre réponse :lol3:!!
Les choses vont mieux quand ils sont simples :we:!!!
-
mathelot
 par mathelot » 03 Jan 2013, 17:02
par mathelot » 03 Jan 2013, 17:02
bonjour,
on montre que

n'a pas de plus petit élément
si
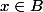
^2 > x^2 - 2 \epsilon x \, > \, 2)
dès lors que

Les majorants de A n'appartiennent pas à A.
sup(A) n'appartient pas à A
Les éléments de B ne sont pas "sup(A)" car B n'a pas de plus petit élement.
sup(A) n'appartient pas à B car
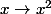
est strictement croissante sur R+*
les élements de B majorent A sans être "sup(A)".
sup(A) n'existe pas (ni dans A, ni dans B).
(A,B) est une coupure (au sens de Dedekind) de

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
