Fonction continue et derivé et borne superieur

par **Yass77** » 09 Sep 2006, 19:46

bonjour a tous ...
Voici un petit probleme.
Soit f une fonction derivable deux fois sur [0,1]. on appelle f' sa derivé premiere et f'' sa derivé seconde
f(0)=0, f(1)=1.
f'(0)=0,f'(1)=0.
on apellera L Sup|f'(t)| .
Montrer que L>1
Montrer ensuite qu'il existe a dans [0,1] tel que |f''(a)|>L²/(L-1).

Je bloque a la deuxieme question .
Merci et bon courage a tous .

par **tize** » 09 Sep 2006, 19:48

Salut Yass77, c'est José(FORUM ESPACE MATH)...tu peux dire merci pour la première...

par **Yass77** » 09 Sep 2006, 19:54

Desolé mais je ne l'ai pas encore lus ... je suis loin d'etre ingrat ..... cependant il se trouve que javais deja trouver un methode pour la premiere en utilisant l'intégrale.
merci beaucoup et puis si tu trouve la deuxieme fait la moi parvenir si possible merci ...

par **tize** » 12 Sep 2006, 18:34

Si quelqun a une solution élégante pour la deuxième question je suis preneur...

par **tize** » 14 Sep 2006, 19:00

Je me permet de faire remonter ce fil pour avoir un peu d'aide...
Pour la première question de Yass77 c'est bon, voilà une preuve (il y a surement beaucoup plus court...)

Soit

et

est continue. Il existe donc

tq

donne

.
On applique alors le TAF avec y dans

:

.
Maintenant par l'absurde on suppose

; en appliquant le TAF avec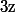

dans

, on a :

Quoi qu'il en soit, on a sur

,

ce qui est absurde puisque

C'est pour la deuxième question...auriez-vous une idée à proposer ?
Merci

par **yos** » 16 Sep 2006, 22:52

Début d'ébauche de commencement de piste.
Avec Taylor Lagrange sur [0,x], on obtient

.
De même sur [x,1] :

.
Si on imagine que f '' est majorée par L²/(L-1), on en tire des majorations de
f(x) ... mais je n'ai pas trouvé de contradiction.
Ca me parait sévère comme exercice et ce message ne sert qu'à le remonter.

par **tize** » 18 Sep 2006, 11:37

yos a écrit:Début d'ébauche de commencement de piste.
Avec Taylor Lagrange sur [0,x], on obtient .
De même sur [x,1] : .
Si on imagine que f '' est majorée par L²/(L-1), on en tire des majorations de
f(x) ... mais je n'ai pas trouvé de contradiction.
Ca me parait sévère comme exercice et ce message ne sert qu'à le remonter.

Oui je trouve aussi...au passage, as tu trouvé une méthode plus élégante pour la première question ?
J'en profite évidement pour faire remonter ce fil... :zen:

par **yos** » 27 Sep 2006, 15:49

Pour la première question, je pense que ton idée est la bonne.
Pour la seconde, j'ai fini par poser la question sur math.net et j'ai obtenu une réponse :ici

par **tize** » 27 Sep 2006, 16:05

Merci pour le lien Yos. Je dois avouer que j'avais arrêté de chercher quelque temps. Je pense que je n'aurai pas trouvé de si tôt.
Merci.

Fonction continue et derivé et borne superieur

fonction continue et derivé et borne superieur

Qui est en ligne