Forum de Mathématiques: Maths-Forum

Excusez moi de vous resoliciter pour le probleme d'arithmétique suivant :

p étant premier (supérieur a 5) , montrer que est la somme de 3 carrés ...

Depuis 2 jours ke l'on m'a posé le probleme, les moqueries fusent... AIdez moi, pour que je garde encire quelque dignité !

Naturellement La solution avec un 0^2 est triviale... mais on écarte ces solutions Sinon oui moi oci ca m'étonne que ce soit dans un livre de Term , mais on me l'a posé en disant ça... certainement mon me rendre rageux , c le cas ! je ne trouve pas ... Je recherche je cherche et espere ke vous me li...

Le probleme est simple : FIgurant dans un livre de terminal S , je mis casse pourtant les dents :

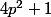
p étant premier (supérieur a 5) , montrer que est la somme de 3 carrés ...

Voila aidez moi SVP merci

Se pose un moi un probleme de simplicité et donc souvent de beauté mathématique ... : Il me faut trouver un équivalent en l'infini de : 1/2pi intégrale de O a 2pi du noyau de Dirichlet d'ordre n Je sais ke l'équivalent est (4/pi carré) ln n mais ma méthode est longue et pas top je donne l'expression...

Pourkoi tant de propo vindicatif ?? je n'est fait ke relancer le sujet ki me casse la tete depuis kelk jour...Je notais juste ke les hyperplans bien kils soient nuageux sont moins séduisants kun bon pb danalyse... Je le déplorais mais continuerais cependant a chercher en espérant ke ca ne stopera pa...

Très décu ke des ke les kestions ne sont plus du genre comment factoriser ce trinome ou calculer une intégrale plus personne n'est o rendez vous pour me prodiguer son aide... Certes le sujet est vague et ardu , mé tout se meme ! Je réénonce le probleme : On sait qu'il est possible de trouver des hyp...

On sait qu'il est possible de trouver des hyperplans denses dans un evn (souvent appelés édredon ou nuage :) ) par exemple : H = { P apartenant a R[X] tel que P(1) = 0 } Est t il possible de former un hyperplan dense grace o Théoreme des résidus qui stipule en gros que si l'intégrale de moins l'infi...

Je suis a la recherche d'un fonction dérivable sur un intervalle de R (D1) et de dériver non continue sur cet intevalle (non C1)
Cela existe-t-il ?
et D2 et non C2 sur int de R ?
C dur dur l'analyse fonctionnelle !
MErci d'avance pour votre aide

Bien jouer !
Jy été preske kan tu la envoyer
Javer kla somme des 0 a n des 1/k - r(n) était égale a 0
Ce ki correspond effectivement a ta derniere ligne.
Mais subsiste pour moi un flou sur la conclusion avec la divergence etc... (jsui pas encore averti en série milles excuses !)
Chapeau l'ami !

OUi oui javé trouver le truc de Rolle et pour l'unicité dcette racine g travaillé avec le nombre de racine et le degré du polynome . Ca ca me semble ok Mais la tache est je pense de prouver la décroissance de r(n) dans un premier temps Peut etre cette nuit méclaireras tel ! Ptite remarque à Alexandr...

Soit le polynome P(n) de X de degré n+1, de racines 0, 1,2,...,n MOntrer kil existe une unique racine r(n) du polynome dérivé entre 0 et 1 et que la suite des r(n) converge vers 0. Voici une énigme ki m'a couté un certain nombre de nuit , je nen puis plus Venez moi en aide , j'ai teriblement besoin ...