Soit le polynome P(n) de X de degré n+1, de racines 0, 1,2,...,n
MOntrer kil existe une unique racine r(n) du polynome dérivé entre 0 et 1 et que la suite des r(n) converge vers 0.
Voici une énigme ki m'a couté un certain nombre de nuit , je nen puis plus Venez moi en aide , j'ai teriblement besoin de dormir ! MErci A les math ca nous rendra dingues
Suite de racine d'un polynome dérivé ! hihi
8 messages
- Page 1 sur 1
C'est dommage de ne plus en dormir, surtout si tu es en prépa ! garde des forces pour la suite, sans te focaliser sur un unique exo !
Pour t'aider, c'est UNIQUEMENT le théorème de Rolle :
P(0)=0=P(1) donc il existe c dans ]0;1[ tel que P'(c)=0 par Rolle, d'où l'existence.
L'unicité c'est encore Rolle : si tu suppose P'(c1)=P'(c2) alors il existe c3 dans ]0;1[ tel que P''(c3)=0 donc P'(c3)=0 ; et par récurrence, P admet une infinité de racine (contradiction avec deg(P')=n )
Pour t'aider, c'est UNIQUEMENT le théorème de Rolle :
P(0)=0=P(1) donc il existe c dans ]0;1[ tel que P'(c)=0 par Rolle, d'où l'existence.
L'unicité c'est encore Rolle : si tu suppose P'(c1)=P'(c2) alors il existe c3 dans ]0;1[ tel que P''(c3)=0 donc P'(c3)=0 ; et par récurrence, P admet une infinité de racine (contradiction avec deg(P')=n )
OUi oui javé trouver le truc de Rolle et pour l'unicité dcette racine g travaillé avec le nombre de racine et le degré du polynome . Ca ca me semble ok
Mais la tache est je pense de prouver la décroissance de r(n) dans un premier temps
Peut etre cette nuit méclaireras tel !
Ptite remarque à Alexandre , tu c jpense ki fo un peu dpassion dans ce monde si "mécanisé" dla prépa... Les exo a la chaine pfff NON A LINDUSTRIE MATHEMATIQUE
Merci de ton aide
Mais la tache est je pense de prouver la décroissance de r(n) dans un premier temps
Peut etre cette nuit méclaireras tel !
Ptite remarque à Alexandre , tu c jpense ki fo un peu dpassion dans ce monde si "mécanisé" dla prépa... Les exo a la chaine pfff NON A LINDUSTRIE MATHEMATIQUE
Merci de ton aide
Je crois avoir trouvé !
On peut poser=\prod_{k=0}^{n}(X-k)) à une constante près...
à une constante près...
on a alors :
=\sum\limits_{k=0}^{n}\prod\limits_{i\neq k}(X-i)) .
.
J'appelle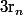 la racine de
la racine de  contenue dans [0;1]. On a :
contenue dans [0;1]. On a :
=\sum\limits_{k=0}^{n}\prod\limits_{i\neq k}(r_n-i)=0) d'ou :
d'ou :
...(r_n-n)+\sum\limits_{k=1}^{n}\prod\limits_{i\neq k}(r_n-i)=0) ou encore :
ou encore :
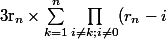=-(r_n-1)...(r_n-n)) et en divisant par
et en divisant par ...(r_n-n)) et par
et par 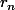 :
:
 le dernier terme étant divergent (serie riemann harmonique) on a nécessairement
le dernier terme étant divergent (serie riemann harmonique) on a nécessairement 
Qu'en pensez-vous ? Il y a une erreur dans mon raisonnement ?
On peut poser
on a alors :
J'appelle
Qu'en pensez-vous ? Il y a une erreur dans mon raisonnement ?
Une démonstration de la divergence de la série 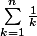 est proposée ici
est proposée ici
une fois que l'on sait cela il suffit de remarquer que : d'ou la divergence de
d'ou la divergence de 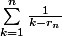
En espérant t'avoir aidé
une fois que l'on sait cela il suffit de remarquer que :
En espérant t'avoir aidé
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
