Bonjour Nightmare
Je crois que tu avais raison.
Par curiosité, qu'aurait donné la comparaison de f(ab) et f(a)*f(b)?
23 résultats trouvés
Revenir à la recherche avancée
- 21 Déc 2009, 22:46
- Forum: ✎✎ Lycée
- Sujet: théorème de bijection
- Réponses: 5
- Vues: 890
Bonsoir,
ah bon ?
car certaines personnes de ma classe m'ont dit qu'il avaient réussi à comparer f(a)*f(b) et f(ab)
ah bon ?
car certaines personnes de ma classe m'ont dit qu'il avaient réussi à comparer f(a)*f(b) et f(ab)
- 17 Déc 2009, 21:13
- Forum: ✎✎ Lycée
- Sujet: théorème de bijection
- Réponses: 5
- Vues: 890
théorème de bijection
Bonjour, Soit k un réel strictement positif. On note f(k) l'unique solution de l'équation exp(x)=k soient a et b deux réels strictement positifs. Comparer f(ab) et f(a)*f(b) ce que j'ai fait : f(k) unique solution de exp(x) = k si et seulement si exp( f(k) ) = k * f(ab) unique solution de exp(x)=ab ...
- 17 Déc 2009, 18:21
- Forum: ✎✎ Lycée
- Sujet: théorème de bijection
- Réponses: 5
- Vues: 890
nombres complexes dans un plan
Bonjour, Je n'arrive pas du tout à faite cet exercice Le plan est muni d'un repère orthonormal direct (O,vecteur u, vecteur v). On choisit 2cm pour unité graphique. Soit f l'application du plan complexe dans lui-même qui à tout point M d'affixe z fait correspondre M' d'affixe z'=z(z barre -4) 1) a) ...
- 22 Nov 2009, 22:37
- Forum: ✎✎ Lycée
- Sujet: nombres complexes dans un plan
- Réponses: 1
- Vues: 755
re
Bonjour
Comment en sachant que 1+x exp(x)
exp(x)
On peut trouver que exp(x)
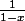
Pouvez juste m'aider pour cette inéquation car moi, je bloque toujours au même endroit, ça m'exaspère.
Je n'arrive pas à faire mieux que exp(-x)
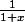
Comment en sachant que 1+x
On peut trouver que exp(x)
Pouvez juste m'aider pour cette inéquation car moi, je bloque toujours au même endroit, ça m'exaspère.
Je n'arrive pas à faire mieux que exp(-x)
- 03 Nov 2009, 07:45
- Forum: ✎✎ Lycée
- Sujet: exercice sur les suites, la fonction exponentielle et des in
- Réponses: 1
- Vues: 1602
exercice sur les suites, la fonction exponentielle et des in
Bonjour à tous J'ai cet exercice à faire : 1°) a)Démontrer que pour tout réel x, 1+x inf ou égal à exp(x) [1] b) en déduire pour tout réel x inf ou égal à 1, exp(x) inf ou égal à 1/(1-x) [2] 2°) a) Déterminer les variation de la fonction cf indice n définie sur [0,+ l'infini[ par cf indice n (x) = x...
- 02 Nov 2009, 13:09
- Forum: ✎✎ Lycée
- Sujet: exercice sur les suites, la fonction exponentielle et des in
- Réponses: 1
- Vues: 1602
re
Bonjour !
Ah d'accord j'ai compris la technique que tu voulais employer Ericovitchi
Mais dans ce cas ce ne serit pas plutôt
A²+B² < 2AB c'est équivalent à (A-B)² <0 ????
car A²+B² -2AB <0
Ah d'accord j'ai compris la technique que tu voulais employer Ericovitchi
Mais dans ce cas ce ne serit pas plutôt
A²+B² < 2AB c'est équivalent à (A-B)² <0 ????
car A²+B² -2AB <0
- 07 Oct 2009, 10:42
- Forum: ✎✎ Lycée
- Sujet: inégalité avec fonction exponentielle VRAI OU FAUX
- Réponses: 7
- Vues: 1873
Bonsoir Angélique
Si je reprends A=B= exp(a)
alors :
exp(2A)+exp(2B)=exp(2*exp(a))+exp(2*exp(a))= 2exp(2*exp(a))
et
2exp(2A+2B)=2exp(2*exp(a)+2*exp(a))= 2exp(4*exp(a))
Donc 2exp(2A+2B) strictement sup à exp(2A)+exp(2B) pour A=B=exp(a)
Donc c'est VRAI
Si je reprends A=B= exp(a)
alors :
exp(2A)+exp(2B)=exp(2*exp(a))+exp(2*exp(a))= 2exp(2*exp(a))
et
2exp(2A+2B)=2exp(2*exp(a)+2*exp(a))= 2exp(4*exp(a))
Donc 2exp(2A+2B) strictement sup à exp(2A)+exp(2B) pour A=B=exp(a)
Donc c'est VRAI
- 06 Oct 2009, 16:09
- Forum: ✎✎ Lycée
- Sujet: inégalité avec fonction exponentielle VRAI OU FAUX
- Réponses: 7
- Vues: 1873
re
Bonsoir
Merci de m'avoir répondue Ericovitchi et Angélique_64
Donc si j'ai compris :
C'est vrai
car on a par exemple :
pour a= exp(2) et b= exp(2)
on a :
exp(2a)+exp(2b) = exp(exp(2))+exp(exp(2))= 3236
et 2*exp(exp(2)+exp(2)=5 237 000.
C'est ça ??
bonne soirée
Julie
Merci de m'avoir répondue Ericovitchi et Angélique_64
Donc si j'ai compris :
C'est vrai
car on a par exemple :
pour a= exp(2) et b= exp(2)
on a :
exp(2a)+exp(2b) = exp(exp(2))+exp(exp(2))= 3236
et 2*exp(exp(2)+exp(2)=5 237 000.
C'est ça ??
bonne soirée
Julie
- 06 Oct 2009, 15:20
- Forum: ✎✎ Lycée
- Sujet: inégalité avec fonction exponentielle VRAI OU FAUX
- Réponses: 7
- Vues: 1873
inégalité avec fonction exponentielle VRAI OU FAUX
Bonjour à tous ! J'ai une "simple" inégalité à résoudre mais je ne trouve pas la réponse. On doit dire si c'est VRAI ou FAUX Il existe un nombre réel a et un nombre réel b, tels que : exp(2a)+exp(2b) strictement inférieure à 2*exp(a+b) Pouvez-vous m'éclairer s'il vous plaît ? Bonne soirée !
- 05 Oct 2009, 16:39
- Forum: ✎✎ Lycée
- Sujet: inégalité avec fonction exponentielle VRAI OU FAUX
- Réponses: 7
- Vues: 1873
Je crois que j'ai compris
pour trouver les valeurs de r, on fait :
8n+2=13n+3
13n-8n=2-3
n=-1/5
Donc r=2/5
Est-ce que c'est juste ?
Je pense que c'est faux car 2/5 est sûrement un entier naturel.
Où est mon erreur ?
pour trouver les valeurs de r, on fait :
8n+2=13n+3
13n-8n=2-3
n=-1/5
Donc r=2/5
Est-ce que c'est juste ?
Je pense que c'est faux car 2/5 est sûrement un entier naturel.
Où est mon erreur ?
- 23 Sep 2009, 16:46
- Forum: ✎✎ Lycée
- Sujet: Petit exercice : Divisibilité et congruence
- Réponses: 2
- Vues: 1156
re
J'ai un peu avancé :
1) b) : r=8n+2
2) b)
r=13n+3
Il manque plus que la question 3
Pouvez-vous m'aider svp ?
1) b) : r=8n+2
2) b)
r=13n+3
Il manque plus que la question 3
Pouvez-vous m'aider svp ?
- 23 Sep 2009, 16:27
- Forum: ✎✎ Lycée
- Sujet: Petit exercice : Divisibilité et congruence
- Réponses: 2
- Vues: 1156
Petit exercice : Divisibilité et congruence
Bonjour à tous ! Pouvez vous me dire si ce que j'ai fait est juste (en italique) et m'aidez à faire le reste svp ? je note # congru 1) Dans la division euclidienne : * de a par 8, le reste est 2 * de a par 104, le reste est r a) démontrer que r#2(8) a#2(8) a#r(104) a#r(13*8) car 104= 13*8 Donc a#r(8...
- 23 Sep 2009, 15:31
- Forum: ✎✎ Lycée
- Sujet: Petit exercice : Divisibilité et congruence
- Réponses: 2
- Vues: 1156
re
OK.
Merci de m'avoir aidée. :++:
A une prochaine fois
Merci de m'avoir aidée. :++:
A une prochaine fois
- 06 Sep 2009, 12:59
- Forum: ✎✎ Lycée
- Sujet: petit problème de raisonnement par récurrence
- Réponses: 10
- Vues: 2440
re
En bleu, ce que j'avais déjà fait, en VIOLEt la suite. On raisonne par récurrence. 1) on initiative pour n=11, 2^11=2048 et 11*100=1100 donc pour n=11, 2^n supérieur ou égal à 100n est vraie donc P(11) est vraie 2) on considère (SUPPOSE) un entier naturel supérieur à 10 ''k'' tel que P(k) est vraie,...
- 06 Sep 2009, 12:05
- Forum: ✎✎ Lycée
- Sujet: petit problème de raisonnement par récurrence
- Réponses: 10
- Vues: 2440
Re
Merci Ericovitchi de m'avoir répondue ( et aux autres aussi)
Ah ok je comprends finalement ce que tu as rédigé.
Donc, est-ce qu'on peut dire que j'ai démontré la propriété héréditaire avec ça ?
Et Qu'il ne me reste seulement à faire la conclusion ?
Je vais rédiger la suite de l'exercice.
Ah ok je comprends finalement ce que tu as rédigé.
Donc, est-ce qu'on peut dire que j'ai démontré la propriété héréditaire avec ça ?
Et Qu'il ne me reste seulement à faire la conclusion ?
Je vais rédiger la suite de l'exercice.
- 06 Sep 2009, 10:32
- Forum: ✎✎ Lycée
- Sujet: petit problème de raisonnement par récurrence
- Réponses: 10
- Vues: 2440
re
Bonjour Ericovitchi et Djmaxgamer
<< J'ai repris la rédaction de mon prof. Mais c'est vrai que ''supposons''' est sans doute mieux aproprié que ''considérons''.
<< Je ne comprends pas comment tu passes de 2^k+2^k à 100k+100k
<< J'ai repris la rédaction de mon prof. Mais c'est vrai que ''supposons''' est sans doute mieux aproprié que ''considérons''.
<< Je ne comprends pas comment tu passes de 2^k+2^k à 100k+100k
- 05 Sep 2009, 16:06
- Forum: ✎✎ Lycée
- Sujet: petit problème de raisonnement par récurrence
- Réponses: 10
- Vues: 2440
Re
Bonjour nightmare Merci de m'avoir répondue. Je crois comprendre ce que tu m'as montrée. en fait, je pense qu'il faut que simplifie 2^k+2^k de manière à obtenir quelquechose de supérieur à 100k+100 Je ne sais pas comment développer cela plus. Sans me donner la réponse, pourrais-tu me donner un indic...
- 05 Sep 2009, 14:36
- Forum: ✎✎ Lycée
- Sujet: petit problème de raisonnement par récurrence
- Réponses: 10
- Vues: 2440
petit problème de raisonnement par récurrence
Bonjour à tous Je dois montrer par un raisonnement par récurrence que 2^n supérieur ou égal à 100n pour tout supérieur à 10 J'ai commencé. Je ne pense pas que ce soit très bien fait. Toutefois, tmon problème est que je bloque pour expliquer la suite. Soit P(n) la propriété : '' 2^n supérieur ou égal...
- 05 Sep 2009, 12:37
- Forum: ✎✎ Lycée
- Sujet: petit problème de raisonnement par récurrence
- Réponses: 10
- Vues: 2440
De nouveau, merci Frednight ! :++: Dans le second cas, si elles grillent, cela induit-il un court-circuit ? J'ai fini l'exercice. Je vous joint ici une capture de l'ennoncé. http://images1.hiboox.com/images/1909/bb6e38f4cf210a822abca6f903ed8dba.jpg 3) RAB = R/2 RBC = R/2 Req = R 4) I = U/R = 12/20 =...
- 06 Mai 2009, 17:40
- Forum: ⚛ Physique
- Sujet: 1èreS exercice électricité, distribution de l'énergie
- Réponses: 7
- Vues: 1933
- 23 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
