Bonjour à tous
J'ai cet exercice à faire :
1°) a)Démontrer que pour tout réel x, 1+x inf ou égal à exp(x) [1]
b) en déduire pour tout réel x inf ou égal à 1, exp(x) inf ou égal à 1/(1-x) [2]
2°)
a) Déterminer les variation de la fonction cf indice n définie sur [0,+ l'infini[ par cf indice n (x) = x^n
b) Déduire de l'inégalité [1], que (1+1/n)^n inf ou égal à exp(x)
c) Déduire de l'inégalité [2], que exp(x) inf ou égal à (1+1/n)^n+1
3°) U est la fonction définie pour tout entier n sup ou égal à 1 par :
Un=(1+1/n)^n
a) démontrer que pour tout entier n sup ou égal à 1:
e-e/n inf ou égal à Un inf ou égal à exp(x)
b) en déduire que u converge vers e
c) Avec la calculatrice donner une valeur approchée de U(0), de U(100) et de U(1000)
Ce que j'ai fait :
1°)
a) Pour démontrer que pour tout réel x, 1+x inf ou égal à exp(x)
On va montrer que 1+x-exp(x) inf ou égal à 0
Soit la fonction telle que h(x)= 1+x-exp(x)
h est dérivable sur l'ensemble des réels comme différence de deux fonctions dérivables sur l'ensemble des réels
h'(x)=1-exp(x)
1-exp(x) sup ou égal à 0
-exp(x) sup ou égal à -1
exp inf ou égal à 0
comme exp(x) est strictement croissant sur l'ensemble des réels :
x inf ou égal à 0
J'ai fait un tableau de variation h est croissante sur ]-l'infini,0] et décroissante sur [0,+l'infini[
h admet un maximum au point d'abscisse 0
h(0)=0
Donc pour tout réel x, h(x) inf ou égal à 0
donc 1+x inf ou égal à exp(x)
2°)
a)
cf(x)= x^n
cf'(x)=nx
Sur [0,+ l'infini[, x sup à 0
donc nx sup à 0 car n sup à 0
donc cf'(x) sup à 0
donc cf est croissante sur [0,+ l'infini[
3°)
b) j'y arrive mais pas complétement
tout les limites sont lorsque n tend vers + l'infini.
lim (1/n)=0
lim 1^n = 1
Bref j'y arrive pas trop
c)
U(100)=2,70
U(1000)=2,71
U(10000)=2,72
Le reste, je n'y arrive pas du tout :triste:
Exercice sur les suites, la fonction exponentielle et des in
2 messages
- Page 1 sur 1
re
Bonjour
Comment en sachant que 1+x exp(x)
exp(x)
On peut trouver que exp(x)
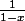
Pouvez juste m'aider pour cette inéquation car moi, je bloque toujours au même endroit, ça m'exaspère.
Je n'arrive pas à faire mieux que exp(-x)
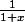
Comment en sachant que 1+x
On peut trouver que exp(x)
Pouvez juste m'aider pour cette inéquation car moi, je bloque toujours au même endroit, ça m'exaspère.
Je n'arrive pas à faire mieux que exp(-x)
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
