Forum de Mathématiques: Maths-Forum

Je reprend:

(car )
et
au voisinage de

enfin, l'intégrale de converge.

Correct ?

Bonjour mathelot

et lorsque

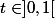
correct ?

Bonjour, ta formule ne m'a pas l'air correct: Si g différentiable en a et f différentiable en g(a), alors fog différentiable en a et d(fog)_a = d(f)_{g(a)} o d(g)_a d'où J(fog) = J(f)_{g(a)}J(g)_a voilà, j'espère que je ne me trompe pas

Bonjour tize et merci de ton aide mais je ne vois toujours pas.
à l'air d'être équivalent à lorsque t -> 0 mais si c'est vrai je n'arrive pas à le prouver.

Bonsoir, j'ai un petit problème d'intégrale f(a) = \int_{0}^{2\pi} ln(a-cos t)dt 1)Montrer que f est bien définie pour a \geq 1 en a > 1, ln(a-cos t) est continue sur [0,2pi]donc intégrable, mais en 1 il faut montrer que \int_{0}^{2\pi} ln(1-cos t)dt converge... c'est là que ...

1/ je suis d'accord 2/Avec les matrices de ces applications il est simple de déterminer la dimension du noyau, il ne reste plus qu'à appliquer le théorème du rang. Pour le reste, t'as une proposition qui dit que E = W1 + W2 (en somme directe) <=> l'intersection de W1 et W2 = {0} et dim W1 + dim W2 =...

Je ne sais pas si ça va t'aider mais tu peux aussi utiliser l'autre définition:

f est dérivable en x0 ssi existe.

Ah mais bien sûr !

sur la droite (x,x) on a

Donc ne tend pas vers 0

merci, j'aurai dû y penser plus tôt >_<

Pour prouver que la dérivée partielle en x n'est pas continue en 0, il faudrait donc la minorer par une fonction qui ne tend pas vers 0 en (0,0) ? ou y at-il une autre méthode ? Si c'est bien ça, je sèche, je ne trouve pas de minoration qui me permettent de conclure... J'ai deux minoration potentiel...

Bonjour, j'ai besoin d'aide pour ces fonctions là: 1)f:R² -> R f(x,y) = \frac{x^3}{x^2+y^2} si (x,y) \not= 0 f(0,0) = 0 Voici mon raisonnement: |\frac{x^3}{x^2+y^2}| < |x| et comme \lim_{(x,y) \to (0,0)}|x| = 0 alors \lim_{(x,y) \to (0,0)}f(...

Merci de ta réponse JQ_

Je retombe bien sur ce résultat :) (j'étais bloqué sur une bête erreur de calcul)

Bonsoir, je bloque sur cet exo qui a pourtant l'air simple: [INDENT]f: R² -> R f(x,y) = (x^4)+(y^4)-(2x^2)+4xy-(2y^2) Trouver les points critiques.[/INDENT] -> En calculant les dérivées partielles je trouve df/dx = 4[(x^3)-x+y] et df/dy = 4[(y^3)-y+x] Cr(f) = {(x,y) de R² | df/dx=df/dy=0 } Bon, on a...