Forum de Mathématiques: Maths-Forum

Je pense avoir résolu le problème, on suppose k < n-1 donc k+1 < n. On dispose donc d'un sommet y du graphe qui n'est pas dans le cycle. Mais alors par connexité du graphe, il existe un indice l et un chemin liant y et a_l. Mais le chemin obtenu est plus grand que le chemin maximal généré par le cyc...

Bonjour, Voici une question que j'ai du mal à traiter : on souhaite prouver le théorème de Dirac sur les graphes : Soit G un graphe fini simple connexe non orienté à n sommets. On suppose que tous les sommets ont degré au moins n/2. Alors G est hamiltonien. A un moment de la preuve, on suppose que l...

Je suis venu, j'ai vu et j'ai vaincu ;) merci. Juste une petite question : je vois que vous êtes sur la plupart des forums de maths, mais comment faites vous pour avoir réponse à presque tout ? L'agreg serait le passage après lequel "tout" deviendrait limpide, ou est ce parce que vous avez...

Bonjour,

Je sais que la somme des racines n ieme de l'unité vaut 0, mais la réciproque est elle vraie? C'est à dire que si l'on a 1+z+z^2+...+z^(n-1) =0, les solutions sont elle nécessairement les racines n ieme de l'unité? Merci bien.

Oui tout à fait. En fait je posais cette question car dans la limite à calculer dans l'exercice, on avait -n en bas et n*ln(x) dans l'exponentielle (ils tendent tous deux vers - infini) et la limite est 0. Par conséquent je me disais que même si les "x" n'ont pas la même expression, la cro...

Ok donc pour utiliser une croissance comparée, les "x" doivent tous avoir la même expression (qui tendent toutes vers -infini) et pas des expressions différentes qui tendent toutes vers - infini

Oui on a effectivement n un entier naturel. Pour le calcul de limite, effectivement il est judicieux de passer en valeur absolue. Non ce que je voulais dire concernait surtout le fait de se ramener à une croissance comparée.
Voyez-vous où je veux en venir dans mon premier message ?

Bonjour, J'ai une question concernant le calcul de la limite suivante : \lim\limits_{n \rightarrow +\infty} (n+1)x^n avec |x|<1 . Cette limite vaut 0 . Je ne peux pas réécrire sous la forme exponentielle x^n car on ne sait pas à priori si x est strictement positif. Mais hormis cela, imaginon...

ok ça marche merci

Ok je crois que c'est bon. En effet, dim E = dim(ker f) + rg(f). Et dim E = dim(ker f²) + rg(f²). Or dim(ker f) = dim(ker f²) par hypothèse. Donc par soustraction, rg(f) = rg(f²). De plus, Im f² inclus dans Im f donc Im f² = Im f. Juste une chose, peut-on écrire dim E = dim(ker f²) + rg(f²) quel que...

Ok el famoso theorema del rang !

Ah ok, car avec f un endomorphisme de L(E) avec E un ev de dimension finie, on me demande de montrer l'équivalence entre plusieurs propriétés parmi lesquelles figurent Ker f = Ker f² et Im f = Im f². Donc je me dis que puisque ces assertions doivent être équivalentes, on doit pouvoir montrer en part...

Bonjour,

On a f un endomorphisme.
Je suppose Ker f² = Ker f. Bon il est clair que Im f² inclus dans Im f. C'est l'autre inclusion qui me pose problème. Merci.

Bonjour,

Soit P un polynôme à coefficients complexes. Quand on écrit , est-ce que ça veut dire pour tout 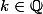ou est-ce que ça veut dire pour tout ?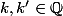

Merci bien.

Ok merci c'est plus clair ! Mais moi je connais juste pour I et J disjoints : 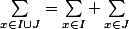. Peut-on se ramener à des unions pour appliquer ceci, ou est-ce une autre règle ?

Bonjour, Dans la formule du crible, on rencontre la notation \sum_{1\leq i_1 < i_2<\ldots <i_k\leq n} . Cela signifie si j'ai bien compris toutes les possibilités de k-uplet possibles d'ensembles que l'on peut former. Ma question est pourquoi cette notation traduit ceci, car je ne vois pas pourquoi....

ça marche !

Ok je vois merci

ok def bernoulli(p): x=np.random.random() if x<=p: return(1) else: return(0) Mais ce que je ne vois pas, c'est pourquoi lorsque la proba x est inférieure à p, alors c'est 1 qui est choisi. Cela vient du fait comme tu l'a dis que la probabilité d'obtenir une probabilité inférieure vaut justement p, m...

Ok, je vais voir cela merci. C'est plutôt np.random.random() à mettre je crois.