94 résultats trouvés
Revenir à la recherche avancée
Re: Petit exercice dérivées partielles
Bonjour, Comme te le dis Pisigma, tes dérivées partielles 1ere, en x et y, sont justes. Pour la dérivée partielle seconde en y, il y a une erreur: il faut dériver une nouvelle fois par rapport à y (pas faire le carré de la dérivée partielle). La fonction alors à dériver est de la forme \frac{1}{u...
- 27 Aoû 2023, 14:11
- Forum: ✯✎ Supérieur
- Sujet: Petit exercice dérivées partielles
- Réponses: 4
- Vues: 217
Re: Exercice de calcul différentiel (niveau L3)
Tout à fait. Tu as raison.
Merci pour les explications détaillées.
L'énoncé doit donc comporter une erreur...
Merci pour les explications détaillées.
L'énoncé doit donc comporter une erreur...
- 28 Juil 2023, 12:48
- Forum: ✯✎ Supérieur
- Sujet: Exercice de calcul différentiel (niveau L3)
- Réponses: 4
- Vues: 681
Re: Exercice de calcul différentiel (niveau L3)
Bonjour, Je te remercie pour les indications qui m'ont permis de conclure. Pour la b), ok mais à quoi sert cette question dans cet exercice? Pour la d), on a: ||Df_{x}(h)||=||h+ Dg_{x}(h)||\leq ||h|| + ||Dg_{x}(h)||\leq (1+k)||h|| Donc Df_{x} est continue et par suite...
- 27 Juil 2023, 15:04
- Forum: ✯✎ Supérieur
- Sujet: Exercice de calcul différentiel (niveau L3)
- Réponses: 4
- Vues: 681
Exercice de calcul différentiel (niveau L3)
Bonjour, J'aurais besoin d'aide pour un exercice de calcul différentiel dont voici l'énoncé Soit\: g : \mathbb{R}^{n}\rightarrow \mathbb{R}^{n} \: \textit{une fonction differentiable telle que:} \: \forall x \in \mathbb{R}^{n},||Dg(x)||\leq k \: \textit{avec } 0<k<1 \textit{On ...
- 26 Juil 2023, 19:20
- Forum: ✯✎ Supérieur
- Sujet: Exercice de calcul différentiel (niveau L3)
- Réponses: 4
- Vues: 681
Re: Permutation de chiffre et divisibilité
Le nombre N en question s'écrit : 1000(k+1) + 100k + 10(k+2) + (k+3) = 1111k + 1023. Mais, 1111k + 1023 = 11(101k + 93). Ceci prouve qu'un tel nombre est divisible par 11. Merci beaucoup! je comprend des choses mais il faut que je bosse plus, et que je sois plus rigoureux Faut pas hésiter à se lanc...
- 26 Déc 2022, 22:30
- Forum: ✎✎ Lycée
- Sujet: Permutation de chiffre et divisibilité
- Réponses: 6
- Vues: 289
Re: Permutation de chiffre et divisibilité
Il n'y a absolument pas besoin des congruences pour résoudre cet exercice. C'est un exercice ne nécessitant que des notions basiques d’arithmétique (niveau 3eme).
- 25 Déc 2022, 21:26
- Forum: ✎✎ Lycée
- Sujet: Permutation de chiffre et divisibilité
- Réponses: 6
- Vues: 289
Re: Permutation de chiffre et divisibilité
Bonjour,
On pose :
- N l'entier formé tel que dans ton énoncé
- k l'entier correspondant au chiffre des centaines du nombre N
1) Comment s'écrivent les chiffres des milliers, des dizaines et des unités de N?
2) Comment peux-tu écrire le nombre N en fonction de k?
3) Conclusion?
On pose :
- N l'entier formé tel que dans ton énoncé
- k l'entier correspondant au chiffre des centaines du nombre N
1) Comment s'écrivent les chiffres des milliers, des dizaines et des unités de N?
2) Comment peux-tu écrire le nombre N en fonction de k?
3) Conclusion?
- 25 Déc 2022, 21:00
- Forum: ✎✎ Lycée
- Sujet: Permutation de chiffre et divisibilité
- Réponses: 6
- Vues: 289
Re: Probabilité 1
Pour en finir avec le sujet: 2. a. Soit 1 \leq n \leq 100 le nombre de cartes tirées. Soit X_i : la variable aléatoire représentant le numéro obtenu au tirage n° i Soit Y : la variable aléatoire représentant le plus grand numéro obtenu parmi les cartes tirées. On a \mathbb{P}(X_i \leq k) = \...
- 13 Déc 2022, 23:54
- Forum: ✯✎ Supérieur
- Sujet: Probabilité 1
- Réponses: 5
- Vues: 250
Re: Les nombres merveilleux de Demlo
Bonsoir, Je suis loin d'être un spécialiste en arithmétique mais voilà quelques pistes. Q3: à partir de p = 10, une retenue vient perturber la symétrie Q4 a) Tu as la liste des 10 premiers nombres merveilleux, et tu connais le critère de divisibilité par 9. Tu peux donc facilement trouver le reste m...
- 10 Déc 2022, 23:59
- Forum: ✎✎ Lycée
- Sujet: Les nombres merveilleux de Demlo
- Réponses: 2
- Vues: 323
Re: Probabilité 1
1.b. De ce qui précède, on établit un résultat intermédiaire: \sum_{k=1}^{100} \mathbb{P}(X=k) = \sum_{k=n}^{100} \mathbb{P}(X=k) =\sum_{k=n}^{100}\frac{\dbinom{k-1}{n-1}}{\dbinom{100}{n}} = 1 Ainsi \sum_{k=n}^{100}{\dbinom{k-1}{n-1} = \dbinom{100}{n} On en déduit: \begin{equation} ...
- 09 Déc 2022, 01:09
- Forum: ✯✎ Supérieur
- Sujet: Probabilité 1
- Réponses: 5
- Vues: 250
Re: Vecteurs: droites sécantes ou non-coplanaires?
Les coordonnées de 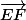 sont encore erronées.
sont encore erronées.
- 08 Déc 2022, 01:05
- Forum: ✎✎ Lycée
- Sujet: Vecteurs: droites sécantes ou non-coplanaires?
- Réponses: 11
- Vues: 408
Re: Probabilité 1
1.a. Soit X : la variable aléatoire représentant le plus grand numéro obtenu parmi les cartes tirées Soit n le nombre de cartes tirées ⋅ \textrm{Si } n=100 \textrm{ cartes} ~\mathbb{P}(X=100)=1 \textrm{ et } \mathbb{P}(X=k)=0 \textrm{ avec } 1 \leq k \leq 99 ~ ⋅ ...
- 06 Déc 2022, 23:20
- Forum: ✯✎ Supérieur
- Sujet: Probabilité 1
- Réponses: 5
- Vues: 250
Re: Vecteurs: droites sécantes ou non-coplanaires?
Pour la question c, c'est la bonne démarche mais les coordonnées de

- 04 Déc 2022, 21:48
- Forum: ✎✎ Lycée
- Sujet: Vecteurs: droites sécantes ou non-coplanaires?
- Réponses: 11
- Vues: 408
Re: Vecteurs: droites sécantes ou non-coplanaires?
Oui,tout à fait!
- 04 Déc 2022, 19:29
- Forum: ✎✎ Lycée
- Sujet: Vecteurs: droites sécantes ou non-coplanaires?
- Réponses: 11
- Vues: 408
Re: Vecteurs: droites sécantes ou non-coplanaires?
1) Écris les représentations paramétriques des droites (AB) et (CD) Les droites sont soit sécantes, soit non-coplanaires, comme tu l'as bien remarqué. 2) Si elles sont sécantes, leur point d'intersection doit vérifier les 2 équations paramétriques.. Essaie de voir si c'est possible. 3) Conclus ;)
- 04 Déc 2022, 18:48
- Forum: ✎✎ Lycée
- Sujet: Vecteurs: droites sécantes ou non-coplanaires?
- Réponses: 11
- Vues: 408
Re: Vecteurs: droites sécantes ou non-coplanaires?
Bonjour,
Avez-vous vu les équations paramétriques de droites?
Avez-vous vu les équations paramétriques de droites?
- 04 Déc 2022, 17:17
- Forum: ✎✎ Lycée
- Sujet: Vecteurs: droites sécantes ou non-coplanaires?
- Réponses: 11
- Vues: 408
Re: Probabilité 1
Bonjour, Pour la question 1: Comme te l'a conseillé lycéen95, il faut y aller par étapes pour dégager une formule. Considère déjà les cas simples où la personne tire sans remise: ⋅ n=100 \textrm{ cartes} ⋅ n=99 \textrm{ cartes} ⋅ n=98 \textrm{ cartes} Dans chacun de ...
- 02 Déc 2022, 13:18
- Forum: ✯✎ Supérieur
- Sujet: Probabilité 1
- Réponses: 5
- Vues: 250
Re: Systèmes & Dérivé partielle à 12 dimensions
Bonjour,
Pourrais tu nous expliquer dans quel cadre tu dois faire ce travail?
- Que représente la fonction P?
- Les variables p et Q?
- Les variables et
et  ?
?
Pourrais tu nous expliquer dans quel cadre tu dois faire ce travail?
- Que représente la fonction P?
- Les variables p et Q?
- Les variables
- 30 Nov 2022, 13:19
- Forum: ✯✎ Supérieur
- Sujet: Systèmes & Dérivé partielle à 12 dimensions
- Réponses: 7
- Vues: 186
Re: suite de compacts
La suite x_{\phi(n)} vérifie \forall n \geq 1 , \, x_{\phi(n)} \in K_n \textrm{ car } \phi(n) \geq n . Plus précisément: \forall n \geq 1 ,~ \exists ~N \geq 1 , \forall k \ge N ,~ x_{\phi(k)} \in K_{\phi(k)} \subset K_n Merci encore Issoram. Merci à toi pour ...
- 28 Nov 2022, 22:00
- Forum: ✯✎ Supérieur
- Sujet: suite de compacts
- Réponses: 16
- Vues: 418
Re: suite de compacts
Bonjour,
Oui c'était l'idée: à partir d'un certain rang, comme les compacts sont emboîtés, les éléments de la suite sont tous dans "le compact suivant". Ton idée d'extractions successives de sous-suites revient presque au même finalement, en un peu plus compliqué.
Oui c'était l'idée: à partir d'un certain rang, comme les compacts sont emboîtés, les éléments de la suite sont tous dans "le compact suivant". Ton idée d'extractions successives de sous-suites revient presque au même finalement, en un peu plus compliqué.
- 27 Nov 2022, 14:37
- Forum: ✯✎ Supérieur
- Sujet: suite de compacts
- Réponses: 16
- Vues: 418
- 94 résultats trouvés - Page 1 sur 5 • 1, 2, 3, 4, 5
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
