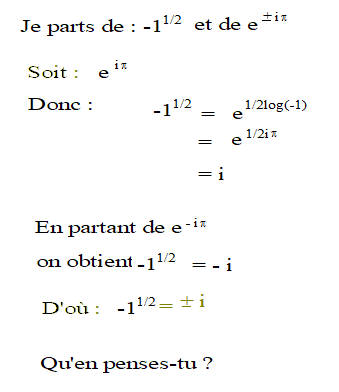27 résultats trouvés
Revenir à la recherche avancée
Re: Pourquoi le mathématique n'aime pas le temps?
Et moi, je n'avais pas remarqué non plus l'ancienneté de ce message initial. Est-il inconvenant de : - Tenter une explication à quelqu'un avec le seul souci de l'aider ? Même avec retard ? - Mon commentaire était-il faux ? - Existe-t-il une date limite de publication d'un sujet à partir de laquelle ...
- 30 Jan 2020, 13:20
- Forum: ⚜ Salon Mathématique
- Sujet: Pourquoi le mathématique n'aime pas le temps?
- Réponses: 15
- Vues: 1045
Re: Pourquoi le mathématique n'aime pas le temps?
Bah, c'est juste que Ptolémée déterre un sujet sans queue ni tête et mort depuis longtemps. Bonjour, Alors là, je suis perplexe ! Est-ce moi l'auteur du texte initial qui a déterré ce sujet ? Non ! Est-ce un crime que répondre à un message sous prétexte qu'il ne vaut rien et de tenter d'expliquer p...
- 30 Jan 2020, 10:37
- Forum: ⚜ Salon Mathématique
- Sujet: Pourquoi le mathématique n'aime pas le temps?
- Réponses: 15
- Vues: 1045
Re: Pourquoi le mathématique n'aime pas le temps?
Bonjour a tous, Pourquoi le mathématique n'aime pas le temps? Pourquoi en dis que le mathématiques est intemporel ? Merci pour vos réponses. Par exemple Il est impossible de faire une bijection entre deux ensembles de nombres différents en mathématiques. Par exemple l'ensemble du nombre de 4 bit et...
- 30 Jan 2020, 08:21
- Forum: ⚜ Salon Mathématique
- Sujet: Pourquoi le mathématique n'aime pas le temps?
- Réponses: 15
- Vues: 1045
Re: Cerveau & écoulement du Temps
Bonsoir à tous. Voici une question qui n'a peut-être aucune réponse... Quelles sont les cellules, quels sont les neurones du cerveau qui sont responsables de la perception du Temps qui s'écoule ? Bonjour, Tant que la physique n'aura pas découvert la nature du Temps ( car c'est avant tout une questi...
- 30 Jan 2020, 06:03
- Forum: ☤ Biologie
- Sujet: Cerveau & écoulement du Temps
- Réponses: 13
- Vues: 3947
Re: Sur la racine carrée de i.
Le passage par les logarithmes ne change rien au problème : De la même façon qu'on a de gros soucis à définir la racine d'un complexe a du fait que l'équation z^2\!=\!a admet plusieurs solutions (à savoir deux), ben on a exactement le même problème pour définir le logarithme d'un complexe du fait q...
- 29 Jan 2020, 13:34
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
Re: Sur la racine carrée de i.
Le passage par les logarithmes ne change rien au problème : De la même façon qu'on a de gros soucis à définir la racine d'un complexe a du fait que l'équation z^2\!=\!a admet plusieurs solutions (à savoir deux), ben on a exactement le même problème pour définir le logarithme d'un complexe du fait q...
- 29 Jan 2020, 10:40
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
Re: Sur la racine carrée de i.
GaBuZoMeu a écrit:Quea deux racines carrées dans
. Ce n'est pas vraiment un scoop. Où veux-tu en venir ?
Je pense que la situation est claire. Pourquoi continuer à tourner autour du pot ?
Je voulais simplement montrer que de -1 puissance 1/2 émerge i come étant sa valeur.
C'est tout.
- 29 Jan 2020, 10:34
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
Re: Cryptologie
si le cryptage est mathématique, il a plutôt 100% de chance qu'il soit décryptable un jour. 100% de chance dîtes-vous ? Êtes-vous sûr ne ne pas parler sans savoir EXACTEMENT de quoi il s'agit! Par exemple, le principe de cryptage par factorisation d'un nombre par deux nombres premiers est connu et ...
- 29 Jan 2020, 09:42
- Forum: ϟ Informatique
- Sujet: Cryptologie
- Réponses: 8
- Vues: 850
- 29 Jan 2020, 09:14
- Forum: ϟ Informatique
- Sujet: Cryptologie
- Réponses: 8
- Vues: 850
- 29 Jan 2020, 06:33
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
Re: Sur la racine carrée de i.
Bon, ptolémée, je t'ai froissé en parlant de "blague". Mais : 1°) ton âge vénérable fait que tu as peut-être un épiderme un peu trop sensible aux vannes qu'on peut envoyer sur un forum ; 2°) relis ton premier message, et dis moi sincèrement : rétrospectivement, vu ce qui s'en est suivi, n...
- 28 Jan 2020, 16:26
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
Re: Sur la racine carrée de i.
Salut, Personnellement, je trouve l'article "bof bof", c'est à dire pas franchement "faux", mais pas très utile à quoi que ce soit non plus : c'est très très long pour ne pas dire grand chose. Ma vision des choses c'est la suivante (et c'est bien ce que l'on trouve délayé dans l...
- 28 Jan 2020, 15:35
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
Re: Sur la racine carrée de i.
Cette explication du fait qu'on n'a pas de morphisme de groupes était déjà dans ce message, puis répétée dans un message suivant .... Sujet: Sur la racine carrée de i. Mieux vaut tard que jamais ;) En déclarant ci-dessus que "j e ne l'avais pas vue ", je reconnais avoir eu tort. Cela dit,...
- 28 Jan 2020, 13:18
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
Re: Sur la racine carrée de i.
GaBuZoMeu a écrit:Cette explication du fait qu'on n'a pas de morphisme de groupes était déjà dans ce message, puis répétée dans un message suivant ....
Sujet: Sur la racine carrée de i.
Mieux vaut tard que jamais
- 28 Jan 2020, 13:12
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
Re: Sur la racine carrée de i.
Bonjour fatal_error, Je ne comprends pas grand chose à ta deuxième question. Pour la première question, on peut toujours choisir une "détermination principale" du logarithme pour un nombre complexe non nul, ce qui revient à prendre une "détermination principale" de l'argument (l...
- 28 Jan 2020, 10:30
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
Re: Sur la racine carrée de i.
Encore une fois, puisque tu n'as pas l'air de comprendre mon objection principale (ce n'est pourtant pas faute de la répéter) : L'utilisation de \sqrt{\cdot} en dehors des réels positifs pose un certain nombre de problèmes dûs au fait qu'il n'y a pas d'application "racine carrée" sur le g...
- 28 Jan 2020, 08:29
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
Re: Coordonnées polaires vectorielles.
Effectivement, les mots "coordonnées polaires" suffisent. L'ajout du qualificatif "vectorielles" est facultatif, et il permet de spécifier un peu plus l'objet mathématique utilisé, même si rarement utilisé dans ce contexte. J'ai simplement utilisé l'expression employée par notre...
- 27 Jan 2020, 11:28
- Forum: ⚜ Salon Mathématique
- Sujet: Coordonnées polaires vectorielles.
- Réponses: 3
- Vues: 1042
Re: Sur la racine carrée de i.
Il est tout aussi vrai que \large \sqrt a\times \sqrt a=a , donc \large \sqrt{-1}\times \sqrt{-1}=-1 et on en tombe pas sur une contradiction. Du coup, ton argument ne fait pas avancer le schmilblick d'un poil et tu tournes en rond. :mrgreen: https://i.goopics.net/800/ae7be.jpg Mais j'ai lu ceci : ...
- 27 Jan 2020, 11:02
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
Re: Sur la racine carrée de i.
Juste un petit détail : a^b*a^c = a^(b+c) Donc -1^(1/2)*-1^1/2 = -1^(1/2+1/2) = -1^1 = -1. Et, dans ce cas, on ne tombe pas sur une contradiction. Je n'ai rien voulu montrer d'autre ! Je ne me prends pas, et ne me suis jamais pris pour un messie. Encore une agression gratuite. Au plaisir de ne plus ...
- 23 Jan 2020, 11:32
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
Re: Sur la racine carrée de i.
Bonjour et adieu Je ne puis rester sans réagir à votre propos un peu top hâtif ! Notations : R(n) désignera le radical. * désignera un produit. Soit alors i² = -1. Donc i = R(-1) Donc : i² = R(-1)*R(-1) (évident, non ?) On a alors : R(-1)*R(-1) = R(-1*-1) = R(1) = 1 donc i² =1 !!! d'où la contradict...
- 23 Jan 2020, 10:49
- Forum: ⚜ Salon Mathématique
- Sujet: Sur la racine carrée de i.
- Réponses: 34
- Vues: 2681
- 27 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :