440 résultats trouvés
Revenir à la recherche avancée
Re: Structure d'anneau de Z/nZ
tu part de l'addition usuelle + sur Z/nZ et tu cherche quelles sont les différentes multiplications x telles que (Z/nZ,+,x) soit un anneau ? Oui c'est ça, je considère le groupe (\mathbb{Z}/n\mathbb{Z},+) et je cherche toutes les lois \times telles que (\mathbb{Z}/n\mathbb{Z},+,\times&#...
- 08 Avr 2020, 18:54
- Forum: ✯✎ Supérieur
- Sujet: Structure d'anneau de Z/nZ
- Réponses: 4
- Vues: 444
Structure d'anneau de Z/nZ
Bonjour, je me demandais quelles sont les structures d'anneaux que l'on peut mettre sur le groupe 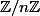 (en plus de la structure habituelle, s'il y en a) ?
(en plus de la structure habituelle, s'il y en a) ?
- 08 Avr 2020, 17:27
- Forum: ✯✎ Supérieur
- Sujet: Structure d'anneau de Z/nZ
- Réponses: 4
- Vues: 444
Re: Correction exercice récurrence
Salut ! Je dis peut-être une bêtise, mais en supposant que n+1 soit impair on devrait avoir n+1 \ge 3, car si on avait n+1 = 1 on aurait n=0 , ce qui n'est pas possible car n\in \mathbb{N}^* . Donc dans l'hypothèse où n+1 serait impair, on a bien n\ge 2 . Bien vu, c'est vrai que finalement pas beso...
- 05 Avr 2020, 15:26
- Forum: ✎✎ Lycée
- Sujet: Correction exercice récurrence
- Réponses: 5
- Vues: 576
Re: Correction exercice récurrence
C'est juste, quelques points par contre : dans la b) ta propriété P(n) ne dépend pas de n, j'imagine que pensais à P(n):n\in A . Ensuite dans l'hérédité, si n+1=2q t'appliques P(q) mais il faut pour ça vérifier que q\leqslant n , c'est vrai car q=\frac{n+1}{2}\leqslant n puisque n\geqslant 1...
- 05 Avr 2020, 01:28
- Forum: ✎✎ Lycée
- Sujet: Correction exercice récurrence
- Réponses: 5
- Vues: 576
Re: Intégration
Multiplie le numérateur et le dénominateur par  , le dénominateur va se simplifier et les racines carrées vont se retrouver au numérateur, ça sera plus simple.
, le dénominateur va se simplifier et les racines carrées vont se retrouver au numérateur, ça sera plus simple.
- 27 Mar 2020, 19:35
- Forum: ✯✎ Supérieur
- Sujet: Intégration
- Réponses: 5
- Vues: 350
Re: Exercice sur les équations fonctionnelles
Montre par récurrence que pour tout n\in\mathbb{N} et pour tout x\in\mathbb{R} , f(\alpha^n x)=f(x)\prod_{k=0}^{n-1}(1-\alpha^k x) , on a alors la même formule pour g . En faisant la différence des deux on a f(\alpha^n x)-g(\alpha ^n x)=(f(x)-g(...
- 25 Mar 2020, 18:43
- Forum: ✯✎ Supérieur
- Sujet: Exercice sur les équations fonctionnelles
- Réponses: 1
- Vues: 427
Re: nombre premier TS spé
Pas besoin de récurrence, il suffit de voir que ^2=2^{2\cdot 2^{n-1}}=2^{2^n}) .
.
- 25 Mar 2020, 18:34
- Forum: ✎✎ Lycée
- Sujet: nombre premier TS spé
- Réponses: 2
- Vues: 289
Re: Question pratique somme avec suites
C'est quoi S ?
- 08 Mar 2020, 22:37
- Forum: ✎✎ Lycée
- Sujet: Question pratique somme avec suites
- Réponses: 4
- Vues: 440
Re: Question pratique somme avec suites
Comme tu veux ça peut même être u_{1789} si tu veux, dans ce cas le 1er terme est u_{1789} le second u_{1790} etc... Si tu veux sommer tes 100 premiers termes alors tu sommeras de u_{1789} à u_{1789+99} , de même si tu choisis que ta suite commence à u_{0} (resp u_{1} ) alors tu sommeras jusqu'à u_{...
- 08 Mar 2020, 21:50
- Forum: ✎✎ Lycée
- Sujet: Question pratique somme avec suites
- Réponses: 4
- Vues: 440
Re: Forme indéterminée (limites)
Si, ta fonction est constante égale à 1...
- 07 Mar 2020, 23:34
- Forum: ✯✎ Supérieur
- Sujet: Forme indéterminée (limites)
- Réponses: 1
- Vues: 272
Re: Calcul Intégrale
Non, il y a toujours le même problème en 0...
- 02 Mar 2020, 04:18
- Forum: ✎✎ Lycée
- Sujet: Calcul Intégrale
- Réponses: 6
- Vues: 548
Re: Probabilité et fonction de densité
Pour la 1) c'est du cours (je crois), la fonction de densité est f(x)=\frac{1}{60-10}=\frac{1}{50} sur [10,60] . La fonction de densité est censée être définie sur \mathbb{R} donc ça serait plutôt f(x)=\frac{1}{50} sur [10,60] et f(x)=0 ailleurs. La 2) c'est une application d...
- 01 Mar 2020, 23:39
- Forum: ✎✎ Lycée
- Sujet: Probabilité et fonction de densité
- Réponses: 1
- Vues: 262
Re: Sommes
Pour le 3) je suis d'accord et pour la 2.1) aussi. Pour la 2.2) c'est presque ça, telle que tu l'as écrite la somme ne contient que 2 termes (ce qui n'est pas le cas), il manque les "..." : 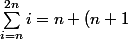+\ldots+(2n-1)+2n) .
.
Re: Calcul Intégrale
Il doit y avoir une erreur d'énoncé : cette intégrale diverge. Pour x\in[0,1],e^x\geqslant 1 donc \frac{e^x}{x^2}\geqslant\frac{1}{x^2} et l'intégrale \int_0^1\frac{dx}{x^2} est divergente ( \lim\limits_{\varepsilon\rightarrow 0}\int_{\varepsilon}^1\frac{dx}{x^2}=+\infty ). Si je me souviens bien en...
- 01 Mar 2020, 02:06
- Forum: ✎✎ Lycée
- Sujet: Calcul Intégrale
- Réponses: 6
- Vues: 548
Re: [Erreur] Convergence Uniforme série exponentielle sur R
Il faut que ton majorant soit indépendant de x ! le tiens : \sum_{n=N+1}^{+\infty}\frac{|x|^n}{n!} dépend de x . Par contre il y a convergence uniforme sur les segments de \mathbb{R} puisque pour A>0 et x\in[-A,A] , \sum_{n=N+1}^{+\infty}\frac{|x|^n}{n!}\leqslant \sum_{n=N+1}^{+\infty}\frac{A^n}{n!}...
- 28 Fév 2020, 02:28
- Forum: ✯✎ Supérieur
- Sujet: [Erreur] Convergence Uniforme série exponentielle sur R
- Réponses: 2
- Vues: 647
Re: Sommes
Est-ce que tu sais comment fonctionne le symbole 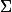 ?
?
Re: Théorème de Beppo Levi
Est-ce que tu connais le théorème de convergence monotone ? ou le théorème de convergence dominée ?
- 20 Fév 2020, 21:00
- Forum: ✯✎ Supérieur
- Sujet: Théorème de Beppo Levi
- Réponses: 2
- Vues: 354
Re: fonction polynôme du 2nd degr, dm de math
En faisant la différence de tes équations on a 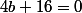 d'où
d'où 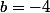 , en reportant dans la première on a
, en reportant dans la première on a  .
.
- 19 Fév 2020, 02:56
- Forum: ✎✎ Lycée
- Sujet: fonction polynôme du 2nd degr, dm de math
- Réponses: 2
- Vues: 491
Re: Maths spé, nombres premiers
Il s'agit du lemme d'Euclide : si p est un nombre premier tel que p|ab alors p|a ou p|b . Il se déduit du lemme de Gauss : si p|a alors c'est fini, si p ne divise pas a alors a et p sont premiers entre eux (si d est le pgcd de a et p alors d|p et p étant premier, on a d=1 ou d=p . Comme de plus d|a ...
- 15 Fév 2020, 15:46
- Forum: ✎✎ Lycée
- Sujet: Maths spé, nombres premiers
- Réponses: 4
- Vues: 554
Re: Continuité et suites de fonctions
La réponse est non, tu es censé savoir que toute fonction continue est approchable uniformément par une fonction en escalier sur un segment, or les fonctions en escalier ne sont pas continues.
- 13 Fév 2020, 21:17
- Forum: ✯✎ Supérieur
- Sujet: Continuité et suites de fonctions
- Réponses: 4
- Vues: 368
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
