Exercice sur les équations fonctionnelles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Georges10
- Membre Relatif
- Messages: 359
- Enregistré le: 23 Avr 2018, 12:01
-
 par Georges10 » 25 Mar 2020, 14:52
par Georges10 » 25 Mar 2020, 14:52
Bonjour à tous. Vous allez bien j'espère.
Ok voici un exercice que j'essaie de traiter mais je suis bloqué à la première question .

J'ai juste besoin d'indications.
Merci d'avance !
-
Tuvasbien
- Membre Relatif
- Messages: 440
- Enregistré le: 28 Fév 2019, 00:59
-
 par Tuvasbien » 25 Mar 2020, 18:43
par Tuvasbien » 25 Mar 2020, 18:43
Montre par récurrence que pour tout

et pour tout
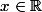
,
=f(x)\prod_{k=0}^{n-1}(1-\alpha^k x))
, on a alors la même formule pour

. En faisant la différence des deux on a
-g(\alpha ^n x)=(f(x)-g(x))\prod_{k=0}^{n-1}(1-\alpha^k x))
. Si on fixe

, alors

car

donc par continuité
-g(\alpha ^n x))=f(0)-g(0)=0)
. Il reste plus qu'a évaluer la limite du produit, je te laisse faire.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités

