Fonction polynôme du 2nd degr, dm de math

[Ineslbmn]

Bonjour,
j'ai un exercice de math qui dit:
les droite d et d' ont respectivement pour équation y=x-1 et y=-x+3
chaque droite a un seul point commun avec la parabole (P) d'équation y=x^2+bx+c
1)Traduire par une relation liant les réels b et c la phrase : la droite d a un seul point commun avec la parabole (P)
Je suis donc partie du principe que pour que la parabole (P) et la droite n'aient qu'un point commun, il faut que le discriminant de l'équation :
x^2+bx+c=x-1
x^2+(b-1)x+c+1=0
soit égale a 0
Je suis donc arrivé a la relation : b^2-2b-4c-3=0 ( cette relation correspond au discriminant qui doit être nul)

2)Déterminer les nombres b et c
Après avoir eu la même démarche en utilisant l'équation de d' et de la parabole (P), j'ai obtenu une seconde relation : b^2+2b-4c+13=0
avec ces 2 relations, j'ai pu déterminer les valeurs de b et c avec b=-4 et c=-11/4

Voila mon problème: après plusieurs vérification de mes calculs, je n'arrive pas à déceler mon erreur... en effet j'ai saisi sur la calculatrice la parabole (P) avec mes valeurs b et c et la courbe obtenu ne correspond pas...
J'ai besoin de votre aide!

[Tuvasbien]

En faisant la différence de tes équations on a 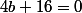d'où 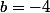, en reportant dans la première on a .

[Ineslbmn]

Merci beaucoup, cela correspond avec ce résultat !