29 résultats trouvés
Revenir à la recherche avancée
salut le programme de spé se compose de l'arithmétique et des matrices .... pour la partie arithmétique il suffit d'avoir un (bon = vrai) niveau collège : c'est à dire savoir calculer (et surtout mentalement, donc en particulier connaître ses tables de multiplication) et penser/raisonner ... Comme ...
- 05 Oct 2015, 20:04
- Forum: ✎✎ Lycée
- Sujet: Importance de la spécialité mathématiques
- Réponses: 5
- Vues: 402
Importance de la spécialité mathématiques
Bonsoir à tous, Je ne suis pas sûr d'être sur le bon forum, donc excusez-moi par avance si j'ai fais une erreur. Je suis actuellement en terminale S spécialité mathématiques et je me demandais si cette spécialité avait une importance dans le tri des classes préparatoires. Je m'explique : je n'appréc...
- 05 Oct 2015, 18:54
- Forum: ✎✎ Lycée
- Sujet: Importance de la spécialité mathématiques
- Réponses: 5
- Vues: 402
J'avais pas fait attention au moins, je me suis focalisé sur les deux quotients -_-
On a donc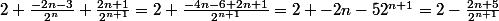
Ce qui permet de justifier l'hérédité du raisonnement par récurrence, merci beaucoup !
On a donc
Ce qui permet de justifier l'hérédité du raisonnement par récurrence, merci beaucoup !
- 21 Sep 2015, 21:49
- Forum: ✎✎ Lycée
- Sujet: Somme des termes d'une suite quelconque
- Réponses: 10
- Vues: 2561
- 21 Sep 2015, 21:28
- Forum: ✎✎ Lycée
- Sujet: Somme des termes d'une suite quelconque
- Réponses: 10
- Vues: 2561
Comment obtenir le dénominateur commun alors? Je pensais que je pouvais passer à (n+1) pour l'autre quotient
- 21 Sep 2015, 21:17
- Forum: ✎✎ Lycée
- Sujet: Somme des termes d'une suite quelconque
- Réponses: 10
- Vues: 2561
bonsoir calcule S ( n+1) = Sn + u( n+1) tu devrais trouver (sauf erreur!) S(n+1)= 2- (2n +5)/2^(n+1) ce qui verifie la formule! Merci de ta réponse, mais je pense avoir un problème parce que quand je développe, je trouve: 2-\frac{2n+3}{2^n}+\frac{2n+1}{2^{n+1}}=2-\frac{2n+5+2n+1}{2^{n+1}}=2-\frac{4...
- 21 Sep 2015, 20:35
- Forum: ✎✎ Lycée
- Sujet: Somme des termes d'une suite quelconque
- Réponses: 10
- Vues: 2561
- 21 Sep 2015, 20:24
- Forum: ✎✎ Lycée
- Sujet: Sens de variation d'une suite
- Réponses: 8
- Vues: 357
Merci de ta réponse rapide, j'avais déjà commencé le raisonnement par récurrence, mais je bloque pour l'hérédité parce que je ne vois vraiment pas ce qu'il faut faire. Initialisation: On veut montrer que la propriété est vraie au rang n=0. \sum_{k=0}^{k=n} u_{k} pour k=0 ; u_{0}=-1 par définition. S...
- 21 Sep 2015, 20:23
- Forum: ✎✎ Lycée
- Sujet: Somme des termes d'une suite quelconque
- Réponses: 10
- Vues: 2561
- 21 Sep 2015, 20:06
- Forum: ✎✎ Lycée
- Sujet: Sens de variation d'une suite
- Réponses: 8
- Vues: 357
Somme des termes d'une suite quelconque
Bonsoir à tous, Je suis en train de faire mon brouillon pour un DM et je reste bloqué sur la dernière question: Pour tout entier naturel n, on pose: S_{n}=\sum_{k=0}^{k=n} (u_{k}=u_{0}+...+u_{n}) . Démontrer par récurrence que pour tout n de N: S_{n}=2-\frac{2n+3}{2^n} Grâce à l'énoncé, on s...
- 21 Sep 2015, 20:04
- Forum: ✎✎ Lycée
- Sujet: Somme des termes d'une suite quelconque
- Réponses: 10
- Vues: 2561
En effet, tu dois t'en servir. Ainsi, tu trouveras un résultat qui te permettra de déterminer si ta suite est croissante ou décroissante.
- 21 Sep 2015, 19:51
- Forum: ✎✎ Lycée
- Sujet: Sens de variation d'une suite
- Réponses: 8
- Vues: 357
Bonjour,
J'espère ne pas faire d'erreur, mais pour étudier le sens de variation d'une suite, il faut faire la différence entre deux termes consécutifs soit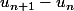 donc tu auras au final
donc tu auras au final 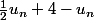 .
.
J'espère ne pas faire d'erreur, mais pour étudier le sens de variation d'une suite, il faut faire la différence entre deux termes consécutifs soit
- 21 Sep 2015, 19:44
- Forum: ✎✎ Lycée
- Sujet: Sens de variation d'une suite
- Réponses: 8
- Vues: 357
A la recherche de conseils pour une orientation post-bac
Bonjour à tous, Je suis actuellement élève en terminale S (spécialité mathématiques) et je me pose quelques questions sur mon orientation. Je pensais que j'avais fixé mon choix en première pour une classe préparatoire MPSI, néanmoins je commence à remettre en question ce choix. Mon projet serait de ...
- 14 Sep 2015, 11:35
- Forum: ➳ Orientation
- Sujet: A la recherche de conseils pour une orientation post-bac
- Réponses: 1
- Vues: 3463
Quelle orientation post-bac ?
Bonjour, Je suis actuellement élève en terminale S et je me pose des questions sur mon orientation. Je tiens à préciser avant tout que ce message ne va peut-être pas traiter exclusivement d'études dans le domaine des mathématiques. Donc voilà, je suis en Terminale S avec de bonnes moyennes de premiè...
- 13 Sep 2015, 19:36
- Forum: ➳ Orientation
- Sujet: Quelle orientation post-bac ?
- Réponses: 1
- Vues: 2616
C'est du calcul algébrique élémentaire : v_{n}=\frac{u_{n}}{u_{n}-1} v_n(u_{n}-1)=u_n v_nu_n-v_n=u_n u_n(v_n-1)=v_n u_n=\frac{v_n}{v_n-1} Expliqué comme ça, je me rends compte que j'ai essayé les chemins les plus compliqués alors que la réponse était très simple. Merci beaucoup pour...
- 05 Sep 2015, 11:00
- Forum: ✎✎ Lycée
- Sujet: Expression d'un suite en fonction de n
- Réponses: 3
- Vues: 519
Expression d'un suite en fonction de n
Bonjour, Un exercice me demande d'exprimer une suite v_{n} et une autre suite u_{n} en fonction de n . On pose v_{n}=\frac{u_{n}}{u_{n}-1} avec u_{0}=-1 pour tout n>=0 . Pour exprimer v_{n} , j'avais une question qui me demander de démontrer que la suite était géométrique donc j'ai calculé la raison...
- 05 Sep 2015, 10:46
- Forum: ✎✎ Lycée
- Sujet: Expression d'un suite en fonction de n
- Réponses: 3
- Vues: 519
zygomatique a écrit:et quelle est la définition d'une suite croissante ?
Une suite est dite croissante si
- 05 Sep 2015, 10:34
- Forum: ✎✎ Lycée
- Sujet: Raisonnement par récurrence
- Réponses: 14
- Vues: 667
1/ que signifie : ? 1'/ quelle propriété de la suite (u_n) demande-t-on de démontrer ? 2/ tu peux donc faire la même chose avec la propriété définie par : ... ? Cela signifie que l'on veut démontrer que la suite est croissante, par contre je ne vois quelle propriété je pourrais citer pour démontrer...
- 04 Sep 2015, 12:15
- Forum: ✎✎ Lycée
- Sujet: Raisonnement par récurrence
- Réponses: 14
- Vues: 667
comment as-tu fait la question 1/ ? Je détaille: J'ai posé la propriété que j'ai cité dans l'énoncé. On vérifie la propriété pour n=1. U_{1}=sqrt(0+5)=sqrt(5) La propriété est vérifiée pour n=1. On suppose que la propriété est vérifiée pour un entier k>=1 . C'est-à-dire que U_{k}\in...
- 03 Sep 2015, 20:12
- Forum: ✎✎ Lycée
- Sujet: Raisonnement par récurrence
- Réponses: 14
- Vues: 667
- 03 Sep 2015, 19:39
- Forum: ✎✎ Lycée
- Sujet: Raisonnement par récurrence
- Réponses: 14
- Vues: 667
- 29 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
